Transition to Turbulence in Fluid Flows
U of M Digital Technology Center's 2010 Digital Technology Initiative Seed Grant
Spotlight
The 2007 Annual Review of Fluid Mechanics article on “Nonmodal Stability Theory” by Peter J. Schmid has devoted two sections to my papers on “Componentwise energy amplification in channel flows”, J. Fluid Mech. 2005, and “The spatio-temporal impulse response of the linearized Navier-Stokes equations”, 2001 American Control Conference. Even though we haven't written a journal version of the impulse response paper, a significantly polished version of the original conference submission can be found in Chapter 10 of my PhD Thesis.
The Annual Review of Fluid Mechanics covers the significant developments in the field of fluid mechanics; its 2012 impact factor is 12.600.
Project synopsis
During my doctoral work, I initiated a system-theoretic approach to model and analyze shear flows of Newtonian fluids, such as air and water. Using this approach I obtained a detailed characterization of the flow structures triggering the transition to turbulence. This is likely to have an impact in a variety of applications including design of fuel-efficient and environmentally-friendly vehicles. Since joining the University of Minnesota, I used this early success as a motivation for a new line of research; this effort resulted in a set of well developed theoretical and computational methods for analysis and control of both Newtonian and non-Newtonian fluids.
In a recent interdisciplinary collaborative effort with Prof. Satish Kumar of Chemical Engineering and Materials Science Department at the University of Minnesota, I have been studying transition to turbulence in shear flows of fluids containing long, flexible, polymer chains. Transition phenomena in these complex viscoelastic fluids are relevant for polymer processing operations and mixing in micro/nano-fluidic devices. Even though such flows are inherently stable when inertial effects are negligible, they often exhibit deviations from laminar profiles impairing quality of polymer products. My research has demonstrated that these deviations are triggered by high flow sensitivity. To counter this sensitivity I have explicitly accounted for modeling imperfections by quantifying their influence on transient and asymptotic dynamics of viscoelastic fluids. My work was the first to reveal previously unknown structural similarities between weakly-inertial flows of viscoelastic fluids and strongly-inertial flows of Newtonian fluids (see figure below for an illustration) and is enhancing the understanding of the early stages of transition to elastic turbulence.
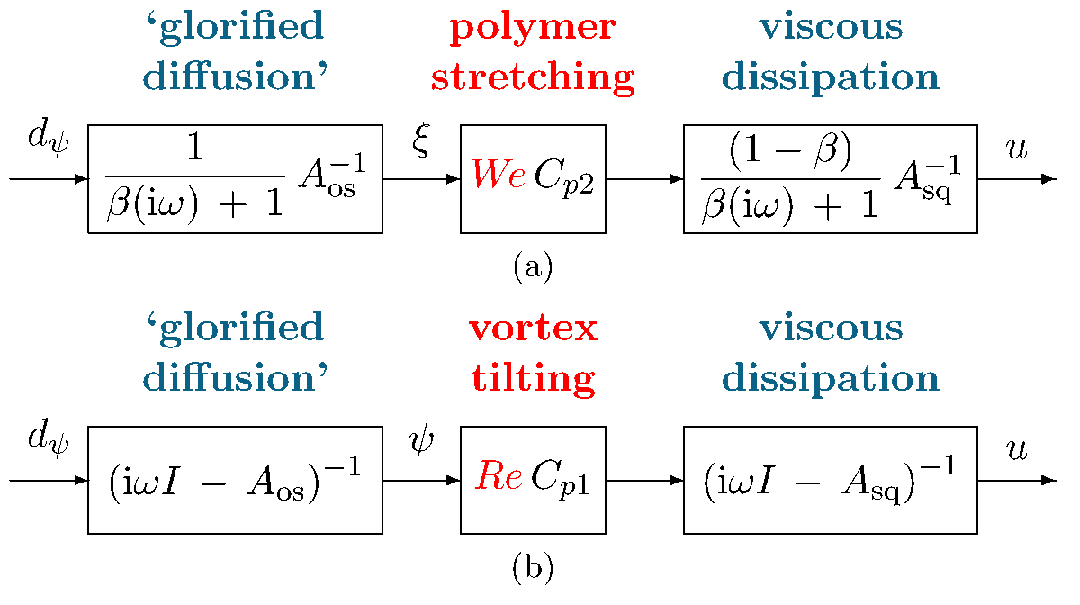 |
Figure 1: Block diagrams of the frequency response operators that map the
wall-normal and spanwise forces to the streamwise velocity fluctuation in
streamwise-constant (a) inertialess flows of viscoelastic fluids; and (b)
inertial flows of Newtonian fluids. In Newtonian fluids amplification originates
from vortex tilting, i.e. the operator 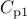 , and in viscoelastic
fluids it originates from polymer stretching, i.e. the operator
, and in viscoelastic
fluids it originates from polymer stretching, i.e. the operator
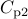 . Note that the Weissenberg number,
. Note that the Weissenberg number, 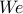 , in
inertialess flows of viscoelastic fluids takes the role of the Reynolds number,
, in
inertialess flows of viscoelastic fluids takes the role of the Reynolds number,
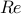 , in inertial flows of Newtonian fluids. Here,
, in inertial flows of Newtonian fluids. Here, 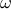 is the temporal
frequency,
is the temporal
frequency, 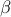 is the viscosity ratio, and
is the viscosity ratio, and 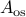 and
and
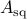 are the streamwise-constant Orr-Sommerfeld and Squire
operators.
are the streamwise-constant Orr-Sommerfeld and Squire
operators.
Relevant Publications
Worst-case amplification of disturbances in inertialess Couette flow of viscoelastic fluids
B. K. Lieu, M. R. Jovanovic, and S. Kumar
J. Fluid Mech., vol. 723, pp. 232-263, 2013.Nonmodal amplification of stochastic disturbances in strongly elastic channel flows
M. R. Jovanovic and S. Kumar
J. Non-Newtonian Fluid Mech., vol. 166, no. 14-15, pp. 755-778, 2011.Transient growth without inertia
M. R. Jovanovic and S. Kumar
Phys. Fluids, vol. 22, no. 2, p. 023101 (19 pages), 2010.Frequency responses of streamwise-constant perturbations in channel flows of Oldroyd-B fluids
N. Hoda, M. R. Jovanovic, and S. Kumar
J. Fluid Mech., vol. 625, pp. 411-434, 2009.Energy amplification in channel flows of viscoelastic fluids
N. Hoda, M. R. Jovanovic, and S. Kumar
J. Fluid Mech., vol. 601, pp. 407-424, 2008.Componentwise energy amplification in channel flows
M. R. Jovanovic and B. Bamieh
J. Fluid Mech., vol. 534, pp. 145-183, 2005.