RETURN                                                                               HOME

The mathematics of electric machine modeling

abc or phase-variable modeling:

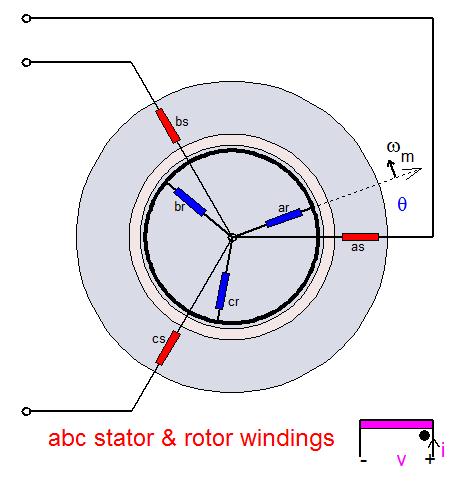
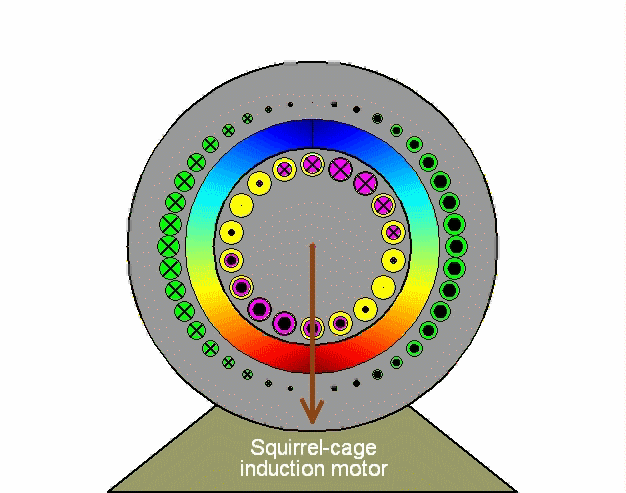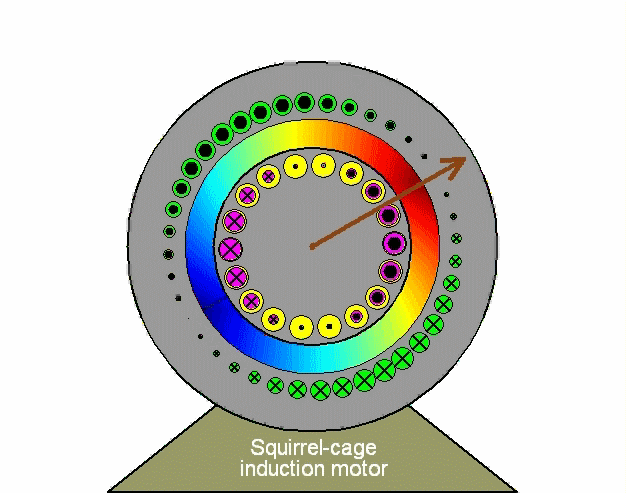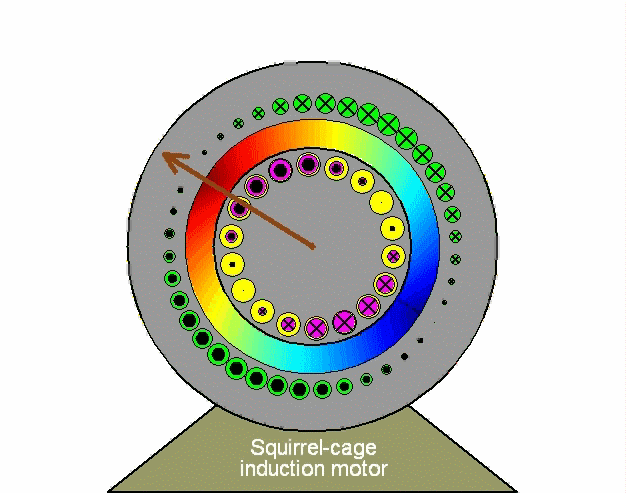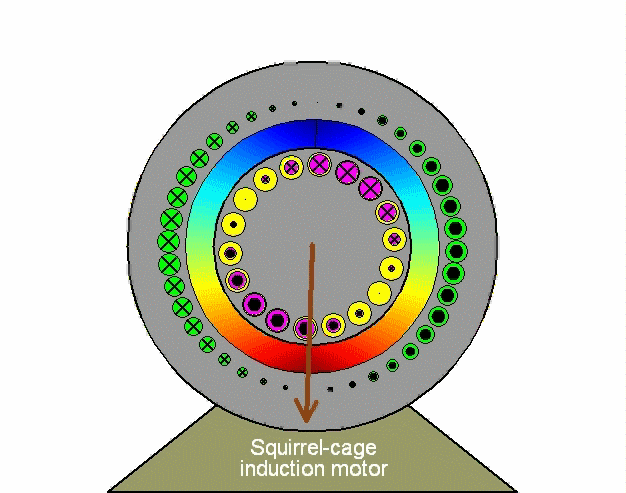
The first step in the mathematical modeling of an induction machine is by describing it as coupled stator and rotor three-phase circuits using phase variables, namely stator currents i_as, i_bs, i_cs and rotor currents i_ar, i_br, i_cr ; in addition to the rotor speed ω_m  and the angular displacement θ between stator and rotor windings. The machine electrical parameters are expressed in terms of a resistance matrix R [6x6] and an inductance matrix L [6x6] in which the magnetic mutual coupling elements are  functions of position θ. The electrical variables V, I, λ appear as 6-element column vectors (in the matrix analysis connotation); so that, for instance, the current vector is I = [i_as i_bs i_cs i_ar i_br i_cr]^t, representing stator and rotor currents expressed in their respective stator and rotor frames. While the matrix analysis of three-phase stator and rotor circuits in relative motion is easy to formulate mathematically (in particular using Matlab), it nevertheless obscures an understanding of the underlying physical interactions and does not directly lead to the introduction of control strategies. To view details of this matrix analysis of an induction machine, press (or open in new window) the following link:

                                                    abc-model 

dq transformations:

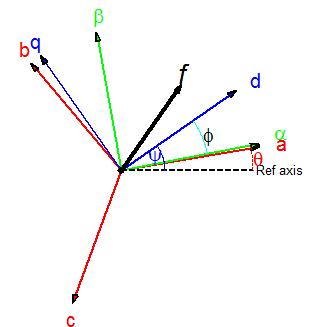
The next step is to transform the original stator and rotor abc frames of reference into a common ω_k or dq frame in which the new variables for voltages, currents, and fluxes can be viewed as space vectors (in a 2-D geometric sense) so that currents are now defined as i_s = [i_ds i_qs] and i_r = [i_dr i_qr]. To view the transformation of variable procedure, press the following link:

                                       dq-transformations 

 dq or space-vector modeling:

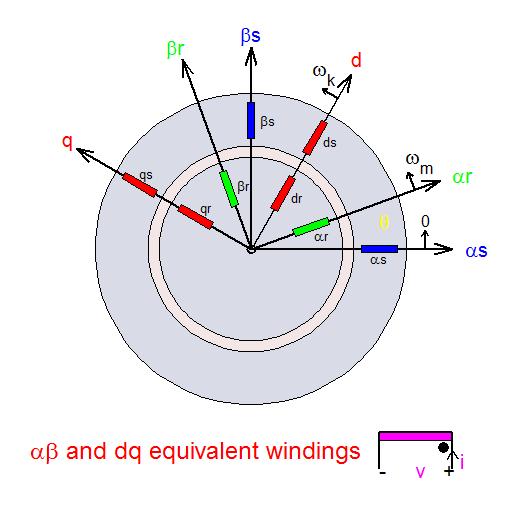
In the dq frame, the inductance parameters become constant, independent of position. Among possible choices of dq frames are the following: a) Stator frame where ω_k = 0; b) Rotor frame where ω_k = ω_m; c) Synchronous frame associated with the frequency ω_s (possibly time varying); d) Rotor flux frame in which the d-axis lines up with the direction of the rotor flux vector. Because it utilizes space vectors, the dq model of the machine provides a powerful physical interpretation of the interactions taking place in the production of voltages and torques, and, more importantly, it leads to the ready adaptation of positional- or speed-control strategies such as vector control and direct torque control. To view details of the space vector modeling, click the following link:

                                     dq-model of the induction machine

dq modeling of the synchronous machine:

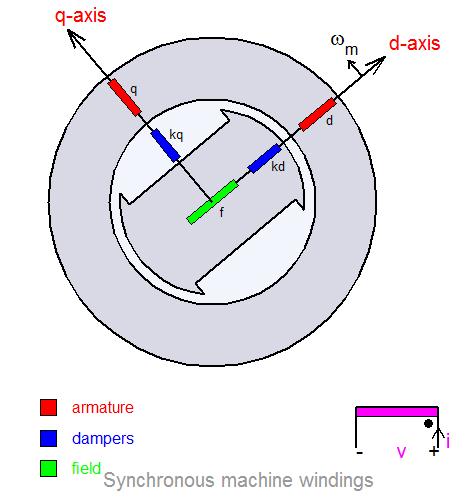
Because of the asymmetry of the synchronous machine created by rotor saliency and field excitation, the corresponding dq model must use the rotor coordinates as reference frame. To view details of the modeling, click the following link:

                                     dq-model of the synchronous machine