CCAMA – A customized alternating minimization algorithm for structured covariance completion problems
 |
Written by:
April 2016 Matlab Files
Papers
|
Purpose
This website provides a Matlab implementation of a customized alternating minimization algorithm (CCAMA) for solving the covariance completion problem (CC). This problem aims to explain and complete partially available statistical signatures of dynamical systems by identifying the directionality and dynamics of input excitations into linear approximations of the system. In this, we seek to explain correlation data with the least number of possible input disturbance channels. This inverse problem is formulated as a rank minimization, and for its solution, we employ a convex relaxation based on the nuclear norm. CCAMA exploits the structure of (CC) in order to gain computational efficiency and improve scalability.
Problem formulation
Consider a linear time-invariant system
![begin{array}{rcl} dot{x} & !! = !! & A , x ; + ; B , u [0.1cm] y & !! = !! & C, x end{array}](eqs/7622844854399723755-130.png)
where 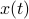 is the state vector,
is the state vector, 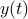 is the output,
is the output, 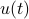 is a
stationary zero-mean stochastic process,
is a
stationary zero-mean stochastic process, 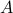 is the dynamic matrix,
is the dynamic matrix, 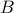 is the input matrix, and
is the input matrix, and 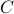 is the output matrix. For Hurwitz
is the output matrix. For Hurwitz 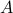 and
controllable
and
controllable 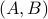 , a positive definite matrix
, a positive definite matrix 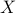 qualifies as the
steady-state covariance matrix of the state vector
qualifies as the
steady-state covariance matrix of the state vector
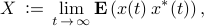
if and only if the linear equation
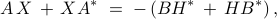
is solvable for 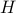 . Here,
. Here, 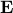 is the expectation operator,
is the expectation operator, 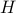 represents the cross-correlation of the state
represents the cross-correlation of the state 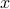 and the input
and the input 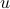 , and
, and  denotes the complex conjugate transpose.
denotes the complex conjugate transpose.
The algebraic relation between second-order statistics of the state and forcing can be used to explain partially known sampled second-order statistics using stochastically-driven LTI systems. While the dynamical generator 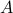 is known, the origin and directionality of stochastic excitation
is known, the origin and directionality of stochastic excitation 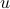 is unknown. It is also important to restrict the complexity of the forcing model. This complexity is quantified by the number of degrees of freedom that are directly influenced by stochastic forcing and translates into the number of input channels or
is unknown. It is also important to restrict the complexity of the forcing model. This complexity is quantified by the number of degrees of freedom that are directly influenced by stochastic forcing and translates into the number of input channels or 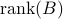 . It can be shown that the rank of
. It can be shown that the rank of 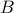 is closely related to the signature of the matrix
is closely related to the signature of the matrix
![begin{array}{rcl} Z &!! mathrel{mathop:}= !!& -(A,X ,+, XA^*) [.15cm] &!! = !!& B H^* ,+, H B^*. end{array}](eqs/8015649963986567082-130.png)
The signature of a matrix is determined by the number of its positive, negative, and zero eigenvalues. In addition, the rank of 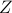 bounds the rank of
bounds the rank of 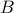 .
.
Based on this, the problem of identifying low-complexity structures for stochastic forcing can be formulated as the following structured covariance completion problem
![begin{array}{cl} {rm minimize} & -{rm log,det}left(Xright) ,+, gamma,||Z||_* [.25cm] {rm subject~to} & ~A , X ,+, X A^* ,+, Z ;=; 0 [.15cm] & ,,left(C X C^* right)circ E ,-, G ;=; 0. end{array} hspace{1.5cm} {rm (CC)}](eqs/8909047710954604432-130.png)
Here, 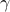 is a positive regularization parameter, the matrices
is a positive regularization parameter, the matrices 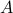 ,
, 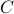 ,
, 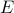 , and
, and 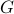 are problem data, and the Hermitian matrices
are problem data, and the Hermitian matrices 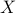 ,
, 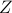 are optimization variables. Entries of
are optimization variables. Entries of 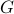 represent partially available second-order statistics of the output
represent partially available second-order statistics of the output 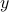 , the symbol
, the symbol  denotes elementwise matrix multiplication, and
denotes elementwise matrix multiplication, and 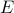 is the structural identity matrix,
is the structural identity matrix,
![E_{ij} ;=; left{ begin{array}{ll} 1, &~ mathrm{if} ~ G_{ij} ~ {rm is~available} [.1cm] 0, &~ mathrm{if}~ G_{ij}~ {rm is~unavailable.} end{array} right.](eqs/3431050645242462279-130.png)
Convex optimization problem (CC) combines the nuclear norm with an entropy function in order to target low-complexity structures for stochastic forcing and facilitate construction of a particular class of low-pass filters that generate colored-in-time forcing correlations. The nuclear norm, i.e., the sum of singular values of a matrix, 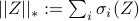 , is used as a proxy for rank minimization. On the other hand, the logarithmic barrier function in the objective is introduced to guarantee the positive definiteness of the state covariance matrix
, is used as a proxy for rank minimization. On the other hand, the logarithmic barrier function in the objective is introduced to guarantee the positive definiteness of the state covariance matrix 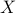 .
.
In (CC), 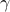 determines the importance of the nuclear norm relative to the logarithmic barrier function. The convexity of (CC) follows from the convexity of the objective function
determines the importance of the nuclear norm relative to the logarithmic barrier function. The convexity of (CC) follows from the convexity of the objective function
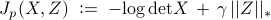
and the convexity of the constraint set. Problem (CC) can be equivalently expressed as follows,
![begin{array}{cl} {rm minimize} & -{rm log,det} X ,+, gamma,||Z||_* [.25cm] {rm subject~to} & ~{cal A}, X ,+, {cal B}, Z ,-, {cal C} ,=, 0, end{array} hspace{1.5cm} {rm (CC}-{rm 1)}](eqs/2120200466362486990-130.png)
where the constraints are now given by
![left[ begin{array}{c} {cal A}_1 {cal A}_2 end{array} right] X ,+, left[ begin{array}{c} I 0 end{array} right] Z ,-, left[ begin{array}{c} 0 G end{array} right] ,=, 0.](eqs/6015843089892321675-130.png)
Here, 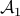 and
and 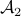 are linear operators, with
are linear operators, with
![begin{array}{c} {cal A}_1(X) ; mathrel{mathop:}= ; A , X ; + ; XA^* [.15cm] {cal A}_2(X) ; mathrel{mathop:}= ; (C , X , C^*)circ E end{array}](eqs/4992472042118422677-130.png)
and their adjoints, with respect to the standard inner product 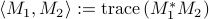 , are given by
, are given by
![begin{array}{c} {cal A}_1^dagger (Y) ; = ; A^* , Y ;+; Y A [.15cm] {cal A}_2^dagger (Y) ; = ; C^* (Ecirc Y) , C. end{array}](eqs/3882247952495856051-130.png)
By splitting 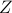 into positive and negative definite parts,
into positive and negative definite parts,
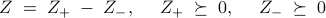
it can be shown that (CC- ) can be cast as an SDP,
) can be cast as an SDP,
![begin{array}{cl} {rm minimize} & -{rm log,det} X ; + ; gamma left( {cal A}, (Z_+) , + , {rm trace}, (Z_-)right) [.25cm] {rm subject~to} & {cal A}_1(X) ,+, Z_+ , - , Z_- ,=, 0 [0.15cm] & {cal A}_2 (X) ,-, G ,=, 0 [0.15cm] & Z_+ , succeq , 0,~~~~Z_- , succeq , 0. end{array} hspace{1.5cm} {rm (P)}](eqs/2697109641737612600-130.png)
The Lagrange dual of (P) is given by
![begin{array}{cl} {rm maximize} & {rm log,det} left( {cal A}_1^dagger(Y_1) , + , {cal A}_2^dagger(Y_2) right) , - ; left<G,, Y_2 right> , + ; n [.25cm] {rm subject~to} & ||Y_1||_2 , leq , gamma end{array} hspace{1.5cm} {rm (D)}](eqs/5952773783997863405-130.png)
where Hermitian matrices 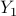 ,
, 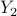 are the dual variables associated with the equality constraints in (P) and
are the dual variables associated with the equality constraints in (P) and 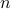 is the number of states.
is the number of states.
Alternating Minimization Algorithm (AMA)
The logarithmic barrier function in (CC) is strongly convex over any compact subset of the positive definite cone. This makes it well-suited for the application of AMA, which requires strong convexity of the smooth part of the objective function.
The augmented Lagrangian associated with (CC- ) is
) is
![begin{array}{l} {cal L}_rho (X, Z; Y_1, Y_2) ; = ; displaystyle{-{rm log,det} X , + , gamma, ||Z||_*} , +, left<Y_1,, {cal A}_1 (X) + Z right> , + , left<Y_2,, {cal A}_2 (X) - G right> ~ + [0.25cm] hfill { displaystyle{ frac{rho}{2}, ||{cal A}_1 (X) , + , Z||_F^2} ; + ; displaystyle{ frac{rho}{2}, ||{cal A}_2 (X) , - , G||_F^2} } end{array}](eqs/5908980935292365493-130.png)
where 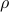 is a positive scalar and
is a positive scalar and 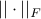 is the Frobenius norm.
is the Frobenius norm.
AMA consists of the following steps:
![begin{array}{rrcl} X-mathbf{minimization}~mathbf{step:} & ~~ X^{k+1} &!!mathrel{mathop:}=!!& {rm argmin}_{X} , {cal L}_0, ( X,, Z^k; , Y_1^k,, Y_2^k) [0.25cm] Z-mathbf{minimization}~mathbf{step:} & ~~ Z^{k+1} &!!mathrel{mathop:}=!!& {rm argmin}_{Z} , {cal L}_{rho}, ( X^{k+1},, Z; , Y_1^k,, Y_2^k) [0.25cm] Y-mathbf{update}~mathbf{step:} & ~~ Y_1^{k+1} &!!mathrel{mathop:}=!!& Y_1^k ,+, displaystyle{rho left( {cal A}_1 (X^{k+1}) , + , Z^{k+1} right)} [0.25cm] & ~~ Y_2^{k+1} &!!mathrel{mathop:}=!!& Y_2^k ,+, displaystyle{rho left( {cal A}_2 (X^{k+1}) , - , G right)} end{array}](eqs/1358873322516725525-130.png)
These terminate when the duality gap
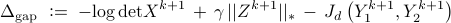
and the primal residual
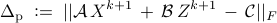
are sufficiently small, i.e., 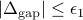 and
and 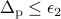 . In the
. In the 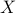 -minimization step, AMA minimizes the Lagrangian
-minimization step, AMA minimizes the Lagrangian 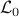 with respect to
with respect to 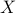 . This step is followed by a
. This step is followed by a 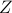 -minimization step in which the augmented Lagrangian
-minimization step in which the augmented Lagrangian 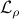 is minimized with respect to
is minimized with respect to 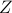 . Finally, the Lagrange multipliers,
. Finally, the Lagrange multipliers, 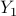 and
and 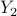 , are updated based on the primal residuals with the step-size
, are updated based on the primal residuals with the step-size 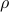 .
.
The 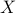 -minimization step amounts to a matrix inversion and the
-minimization step amounts to a matrix inversion and the 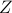 -minimization step amounts to application of the soft-thresholding operator
-minimization step amounts to application of the soft-thresholding operator 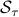 on the singular values of a matrix:
on the singular values of a matrix:
![begin{array}{rcl} X^{k+1} &!!=!!& left( {cal A}_1^dagger (Y_1^k) ,+, {cal A}_2^dagger (Y_2^k) right)^{-1} [0.25cm] Z^{k+1} &!!=!!& {cal S}_tau left( - {cal A}_1 ( X^{k+1} ) , - , (1/rho)Y_1^k right), ~~~~ tau = gamma/rho [0.25cm] Y_1^{k+1} &!!=!!& {cal T}_{gamma} left(Y_1^k ,+, rho, {cal A}_1 (X^{k+1}) right) [0.25cm] Y_2^{k+1} &!!=!!& Y_2^k ,+, displaystyle{rho left( {cal A}_2 (X^{k+1}) , - , G right)} end{array}](eqs/6582258044759247696-130.png)
For Hermitian matrix 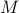 with singular value decomposition
with singular value decomposition 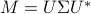 ,
, 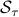 and
and 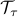 denote the singular value thresholding and saturation operators, respectively:
denote the singular value thresholding and saturation operators, respectively:
![begin{array}{rclrcl} {cal S}_tau (M) &!! mathrel{mathop:}= !!& U , {cal S}_tau (Sigma) ,U^*, & ~~~~ {cal S}_tau (Sigma) &!! = !!& {rm diag} left( left(sigma_i ,-, tau right)_+ right) [.25cm] {cal T}_tau (M) &!! mathrel{mathop:}= !!& U , {cal T}_tau (Sigma) ,U^*, & ~~~~ {cal T}_tau (Sigma) & !! = !! & {rm diag} left( min left( max( sigma_i, -, tau ), tau right) right) end{array}](eqs/7910724952940195208-130.png)
with 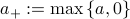 . The updates of Lagrange multipliers guarantee dual feasibility at each iteration, i.e.,
. The updates of Lagrange multipliers guarantee dual feasibility at each iteration, i.e., 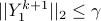 for all
for all 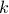 .
.
Alternating Direction Method of Multipliers (ADMM)
In contrast to AMA, ADMM minimizes the augmented Lagrangian in each step of the iterative procedure. In addition, ADMM does not have efficient step-size selection rules. Typically, either a constant step-size is selected or the step-size is adjusted to keep the norms of primal and dual residuals within a constant factor of one another Boyd, et al. ’11.
ADMM consists of the following steps:
![begin{array}{rrcl} X-mathbf{minimization}~mathbf{step:} & ~~ X^{k+1} &!!mathrel{mathop:}=!!& {rm argmin}_{X} , {cal L}_{rho}, ( X,, Z^k; , Y_1^k,, Y_2^k) [0.25cm] Z-mathbf{minimization}~mathbf{step:} & ~~ Z^{k+1} &!!mathrel{mathop:}=!!& {rm argmin}_{Z} , {cal L}_{rho}, ( X^{k+1},, Z; , Y_1^k,, Y_2^k) [0.25cm] Y-mathbf{update}~mathbf{step:} & ~~ Y_1^{k+1} &!!mathrel{mathop:}=!!& Y_1^k ,+, displaystyle{rho left( {cal A}_1 (X^{k+1}) , + , Z^{k+1} right)} [0.25cm] & ~~ Y_2^{k+1} &!!mathrel{mathop:}=!!& Y_2^k ,+, displaystyle{rho left( {cal A}_2 (X^{k+1}) , - , G right)} end{array}](eqs/8647659775536133319-130.png)
which terminate with similar stopping criteria to ADMM.
While the 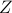 -minimization step is equivalent to that of AMA, the
-minimization step is equivalent to that of AMA, the 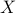 -update in ADMM is obtained by minimizing the augmented Lagrangian. This amounts to solving the following optimization problem
-update in ADMM is obtained by minimizing the augmented Lagrangian. This amounts to solving the following optimization problem
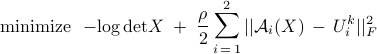
where 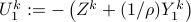 and
and 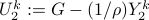 . From first order optimality conditions we have
. From first order optimality conditions we have
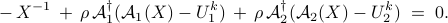
Since 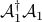 and
and 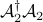 are not unitary operators, the
are not unitary operators, the 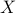 -minimization step does not have an explicit solution. To solve this problem we use a proximal gradient method Parikh and Boyd ’13 to update
-minimization step does not have an explicit solution. To solve this problem we use a proximal gradient method Parikh and Boyd ’13 to update 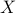 . By linearizing the quadratic term around the current inner iterate
. By linearizing the quadratic term around the current inner iterate 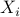 and adding a quadratic penalty on the difference between
and adding a quadratic penalty on the difference between 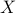 and
and 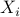 ,
, 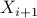 is obtained as the minimizer of
is obtained as the minimizer of
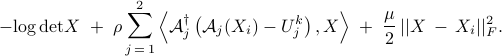
To ensure convergence of the proximal gradient method, the parameter 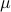 has to satisfy
has to satisfy 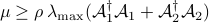 , where we use power iteration to compute the largest eigenvalue of the operator
, where we use power iteration to compute the largest eigenvalue of the operator 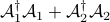 .
.
By taking the variation with respect to 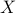 we arrive at the first order optimality condition
we arrive at the first order optimality condition
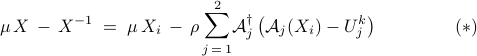
The solution to ( ) can be iteratively computed as
) can be iteratively computed as
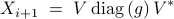
where the 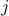 th entry of the vector
th entry of the vector 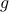 is given by
is given by
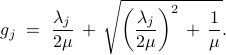
Here, 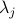 's are the eigenvalues of the matrix on the right-hand-side of (
's are the eigenvalues of the matrix on the right-hand-side of ( ) and
) and 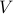 is the matrix of the corresponding eigenvectors. As it is typically done in proximal gradient algorithms Parikh and Boyd ’13, starting with
is the matrix of the corresponding eigenvectors. As it is typically done in proximal gradient algorithms Parikh and Boyd ’13, starting with 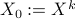 , we obtain
, we obtain 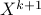 by repeating inner iterations until the desired accuracy is reached.
by repeating inner iterations until the desired accuracy is reached.
Acknowledgements
This project is supported by the
National Science Foundation under Award CMMI 1363266
Air Force Office of Scientific Research under Award FA9550-16-1-0009
University of Minnesota Informatics Institute Transdisciplinary Faculty Fellowship