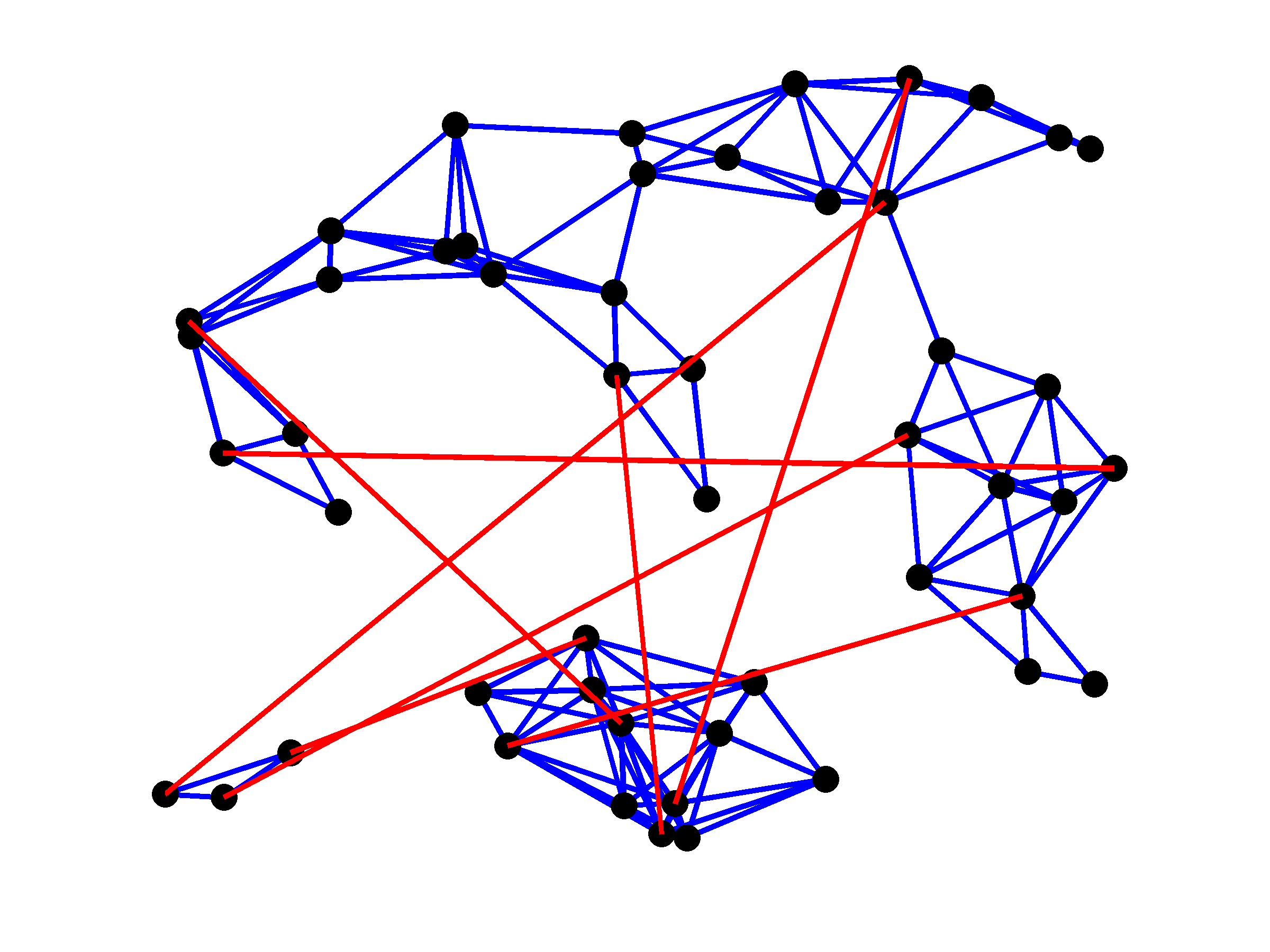
GRAPHSP – Customized algorithms for topology identification and optimal design of noisy networks
 |
Sepideh Hassan-Moghaddam and Mihailo R. Jovanovic May 2016 Matlab Files
Paper
|
Purpose
This website provides a Matlab implementation of customized algorithms for
topology identification and optimal design of undirected consensus networks
with additive stochastic disturbances. By introducing 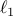 -regularization into
the optimal control formulation aimed at minimizing the steady-state variance
amplification, this problem can be cast as a semidefinite program. Standard
interior-point (IP) method solvers can be used to compute the optimal
solution for small- and medium-size networks. We derive a Lagrange dual and
exploit structure of the optimality conditions for undirected networks to
develop three customized algorithms that are well-suited for large problems.
Our customized algorithms are based on:
-regularization into
the optimal control formulation aimed at minimizing the steady-state variance
amplification, this problem can be cast as a semidefinite program. Standard
interior-point (IP) method solvers can be used to compute the optimal
solution for small- and medium-size networks. We derive a Lagrange dual and
exploit structure of the optimality conditions for undirected networks to
develop three customized algorithms that are well-suited for large problems.
Our customized algorithms are based on:
the infeasible primal-dual IP method;
the proximal gradient method;
the proximal Newton method.
The proximal gradient algorithm is a simple first-order method that updates
the controller graph Laplacian via convenient use of the soft-thresholding operator.
In the IP method, the Newton direction
is obtained using an inexact iterative procedure based on the preconditioned
conjugate gradients and, in the proximal Newton method it is computed using
cyclic coordinate descent over the set of active variables.
We illustrate that all of our algorithms significantly outperform the
general-purpose solvers and greedy strategies and that the proximal algorithms can solve the problems
with more than million edges in the controller graph in a few minutes, on a PC. We also exploit
structure of connected resistive networks to demonstrate how additional edges
can be systematically added in order to minimize the 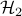 norm of the
closed-loop system.
norm of the
closed-loop system.
Problem formulation
We consider a control problem for undirected consensus
networks with 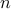 nodes
nodes
![begin{array}{rcl} dot{psi} & !! = !! & - L_p , psi ; + ; u ; + ; d [0.15cm] zeta & !! = !! & left[ begin{array}{c} Q^{1/2} 0 end{array} right] psi ; + ; left[ begin{array}{c} 0 R^{1/2} end{array} right] u [0.35cm] u & !! = !! & - L_x , psi end{array}](eqs/3187735275547866756-130.png)
where 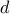 and
and 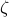 denote disturbance input and performance output,
denote disturbance input and performance output,
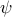 is the state of the network, and
is the state of the network, and 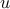 is the control input. Symmetric
is the control input. Symmetric
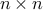 matrices
matrices 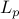 and
and 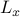 are Laplacians of the plant and the
controller, and matrices
are Laplacians of the plant and the
controller, and matrices 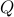 and
and 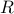 denote state and control weights in
the optimal control problem. Upon closing the loop we obtain
denote state and control weights in
the optimal control problem. Upon closing the loop we obtain
![begin{array}{rcl} dot{psi} & !! = !! & - left( L_p , + , L_xright) psi ; + ; d [0.15cm] zeta & !! = !! & left[ begin{array}{c} Q^{1/2} - R^{1/2} L_x end{array} right] psi. end{array}](eqs/1398749917251800386-130.png)
Our objective is to identify the optimal topology for 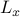 and to design
the corresponding edge weights
and to design
the corresponding edge weights 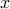 in order to achieve the desired tradeoff
between controller sparsity and network performance. The performance is
quantified by the steady-state variance amplification of the
stochastically-forced network (from the white-in-time input
in order to achieve the desired tradeoff
between controller sparsity and network performance. The performance is
quantified by the steady-state variance amplification of the
stochastically-forced network (from the white-in-time input 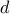 to the
performance output
to the
performance output 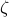 which penalizes deviation from consensus and
control effort).
which penalizes deviation from consensus and
control effort).
To achieve consensus in the absence of disturbances, the closed-loop network has to be connected. This amounts to positive definiteness of the ‘‘strengthened’’ graph Laplacian of the closed-loop network
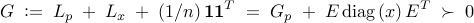
where 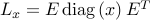 ,
, 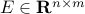 is the given incidence matrix of the
controller graph,
is the given incidence matrix of the
controller graph, 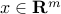 is the vector of controller edge
weights, and
is the vector of controller edge
weights, and
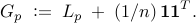
Structural restrictions on the Laplacian matrices introduce an additional
constraint on 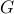 ,
,
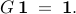
Sparsity-promoting optimal control problem
The steady-state amplification of white-in-time disturbances is determined
by the 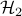 norm of stochastically-forced network,
norm of stochastically-forced network,
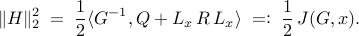
The objective function 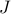 can be expressed as
can be expressed as
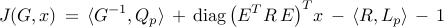
where
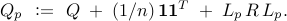
The problem of designing a controller graph that provides an optimal tradeoff
between the 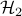 performance of the closed-loop network and the
controller sparsity can be formulated as
performance of the closed-loop network and the
controller sparsity can be formulated as
![begin{array}{rl} {rm minimize} & langle{G^{-1},Q_p}rangle , + ; ensuremath{mathrm{diag}} left( E^{T} R , E right)^T ! x ; + ; gamma ; | x |_1 [0.25cm] {rm subject~to} & G_p , + , E , ensuremath{mathrm{diag}} , ( x ) , E^{T} , succ , 0 end{array} hspace{1.cm} {rm (SP)}](eqs/5752476154995295814-130.png)
where the 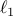 norm of
norm of 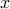 ,
,
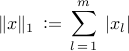
is introduced as a proxy for inducing sparsity. In (SP), the
positive definite matrix 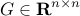 and the vector of the
edge weights
and the vector of the
edge weights 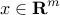 are optimization variables; the problem data
is given by the positive regularization parameter
are optimization variables; the problem data
is given by the positive regularization parameter 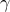 , the plant graph
Laplacian
, the plant graph
Laplacian 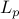 , the state and control weights
, the state and control weights 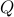 and
and 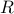 , and the incidence
matrix of the controller graph
, and the incidence
matrix of the controller graph 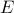 .
.
Since minimization of the Lagrangian associated with (SP) does not lead to an
explicit expression for the dual function, we introduce an auxiliary variable
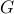 and find the dual of. It is well-known that the consensus can be achieved
even if some edge weights take negative values; e.g., see
Xiao and Boyd ’04. By
expressing the vector of the edge weights,
and find the dual of. It is well-known that the consensus can be achieved
even if some edge weights take negative values; e.g., see
Xiao and Boyd ’04. By
expressing the vector of the edge weights, 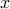 , as a difference between two
non-negative vectors,
, as a difference between two
non-negative vectors, 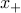 and
and 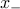 ,
,
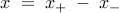
the optimal control problem can be expressed as
![!! begin{array}{rl} {rm minimize} & !! langle{G^{-1},Q_p}rangle , + , (gamma , mathbf{1} , + , {rm diag} left( E^{T} R , E right))^T x_{+} , + , (gamma , mathbf{1} , - , {rm diag} left( E^{T} R , E right))^T x_{-} [0.25cm] {rm subject~to} & !! G , - , G_p , - , E , {rm diag} , ( x_+ , - , x_- ) , E^{T} , = , 0 [.15cm] & !! G , succ , 0, ~~ x_{+} , geq ,0, ~~ x_{-} , geq ,0 end{array} hspace{1.cm} {rm (P)}](eqs/824700062862816455-130.png)
The Lagrange dual of the sparsity-promoting optimal control problem (P) is given by
![begin{array}{rl} {rm maximize} & 2 , {rm trace} left( ( Q_p^{1/2} , Y , Q_p^{1/2})^{1/2} right) , - ; langle{Y,G_p} rangle [0.25cm] {rm subject~to} & |, {rm diag} left( E^{T} (Y ,-, R) , E right) |_{infty} , leq , gamma [0.15cm] & Y ; succ ; 0, ~~ Y , mathbf{1} ;=; mathbf{1} end{array} hspace{1.cm} {rm (D)}](eqs/6479343208385178639-130.png)
where 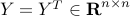 is the dual variable
associated with the equality constraint in (P).
is the dual variable
associated with the equality constraint in (P).
Growing connected resistive networks
The problem of topology identification and optimal design of stochastically-forced networks has many interesting variations. An important class of problems is given by resistive networks in which all edge weights are restricted to be non-negative. Here, we study the problem of growing connected resistive networks. In this, the plant graph is connected and there are no joint edges between the plant and the controller graphs. In the absence of the sparsity-promoting term, the closed-loop network is given by a complete graph. Our objective is to add a small number of edges in order to optimally enhance the closed-loop performance.
The restriction on connected plant graphs implies positive definiteness of the strengthened graph Laplacian of the plant,
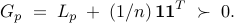
Thus,
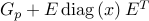 is always positive definite for connected resistive networks.
As done in problem (P), in order to determine the Lagrange dual of the
optimization problem, we introduce an additional optimization variable
is always positive definite for connected resistive networks.
As done in problem (P), in order to determine the Lagrange dual of the
optimization problem, we introduce an additional optimization variable 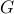 .
The sparsity-promoting optimal control problem simplifies to
.
The sparsity-promoting optimal control problem simplifies to
![begin{array}{rl} {rm minimize} & langle{G^{-1},Q_p}rangle , + , ( gamma , mathbf{1} ,+, {rm diag} left( E^{T} R , E right) )^T x [0.25cm] {rm subject~to} & G , - , G_p , - , E , {rm diag} , (x) , E^{T} , = , 0 [.15cm] & x , geq , 0 end{array} hspace{1.cm} {rm (P1)}](eqs/5879439396998557313-130.png)
where the matrix 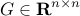 and the vector
and the vector 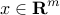 are optimization variables. Non-negativity of the edge weights was
used to write
are optimization variables. Non-negativity of the edge weights was
used to write 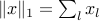 and to remove positive definite
requirements on
and to remove positive definite
requirements on 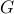 .
.
The Lagrange dual of the sparsity-promoting optimal control problem 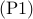 is given by
is given by
![begin{array}{rl} !!!! {rm maximize} & 2 , {rm trace} left( ( Q_p^{1/2} , Y , Q_p^{1/2})^{1/2} right) , - ; langle{Y,G_p}rangle [0.25cm] !!!! {rm subject~to} & {rm diag} left( E^{T} (Y ,-, R) , E right) ; leq ; gamma , mathbf{1} [0.2cm] !!!! & Y ; succ ; 0, ~~ Y , mathbf{1} ;=; mathbf{1} end{array} hspace{1.25cm} {rm (D1)}](eqs/1360184711982162534-130.png)
where 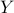 is the dual variable associated with the equality constraint in
is the dual variable associated with the equality constraint in
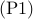 .
.
Acknowledgements
This project is supported by the
National Science Foundation under Award ECCS-1407958 (Program Director: Dr. Kishan Baheti)
University of Minnesota Informatics Institute Transdisciplinary Faculty Fellowship