Two-dimensional channel flow
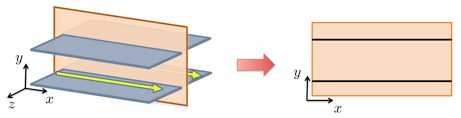 |
Geometry of a two-dimensional channel flow. |
The Orr-Sommerfeld equation governs the dynamics of two-dimensional velocity fluctuations around the laminar channel flow,
![begin{array}{rcl} Delta psi_{t} (k_x, y, t) & !! = !! & left( {displaystyle frac{1}{Re}} , Delta^{2} , - , mathrm{i} , k_x , U(y) , Delta , + , mathrm{i} , k_x , U''(y) right) psi(k_x, y, t) [0.5cm] 0 & !! = !! & psi(k_x, pm 1, t) ; = ; psi' (k_x, pm 1, t) end{array}](eqs/1808209382412542392-130.png)
where
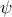 | — | streamfunction |
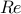 | — | Reynolds number |
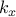 | — | streamwise wavenumber |
![y in left[ -1, 1 right]](eqs/2707710316392746260-130.png) | — | wall-normal coordinate |
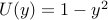 | — | base flow |
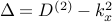 | — | Laplacian |
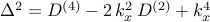 | — | ‘‘square’’ of the Laplacian |
For 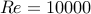 (based on the centerline velocity and
the channel half-width), the discretized version of the Orr-Sommerfeld
equation is obtained using the pseudo-spectral scheme with
(based on the centerline velocity and
the channel half-width), the discretized version of the Orr-Sommerfeld
equation is obtained using the pseudo-spectral scheme with 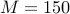 colocation points in the wall-normal direction. Flow fluctuations with
colocation points in the wall-normal direction. Flow fluctuations with
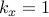 are then advanced in time using the matrix exponential with
time step
are then advanced in time using the matrix exponential with
time step 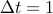 and randomly generated initial profile (that
satisfies both homogeneous Dirichlet and Neumann boundary conditions).
After a transient period of ten time-steps,
and randomly generated initial profile (that
satisfies both homogeneous Dirichlet and Neumann boundary conditions).
After a transient period of ten time-steps, 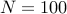 snapshots are
taken to form the snapshot matrices and apply the standard DMD algorithm
along with its sparsity-promoting variant.
snapshots are
taken to form the snapshot matrices and apply the standard DMD algorithm
along with its sparsity-promoting variant.
 |
(a) Spectrum of the Orr-Sommerfeld operator (circles) along with the
eigenvalues resulting from the standard DMD algorithm (crosses) for the
2D channel flow with |
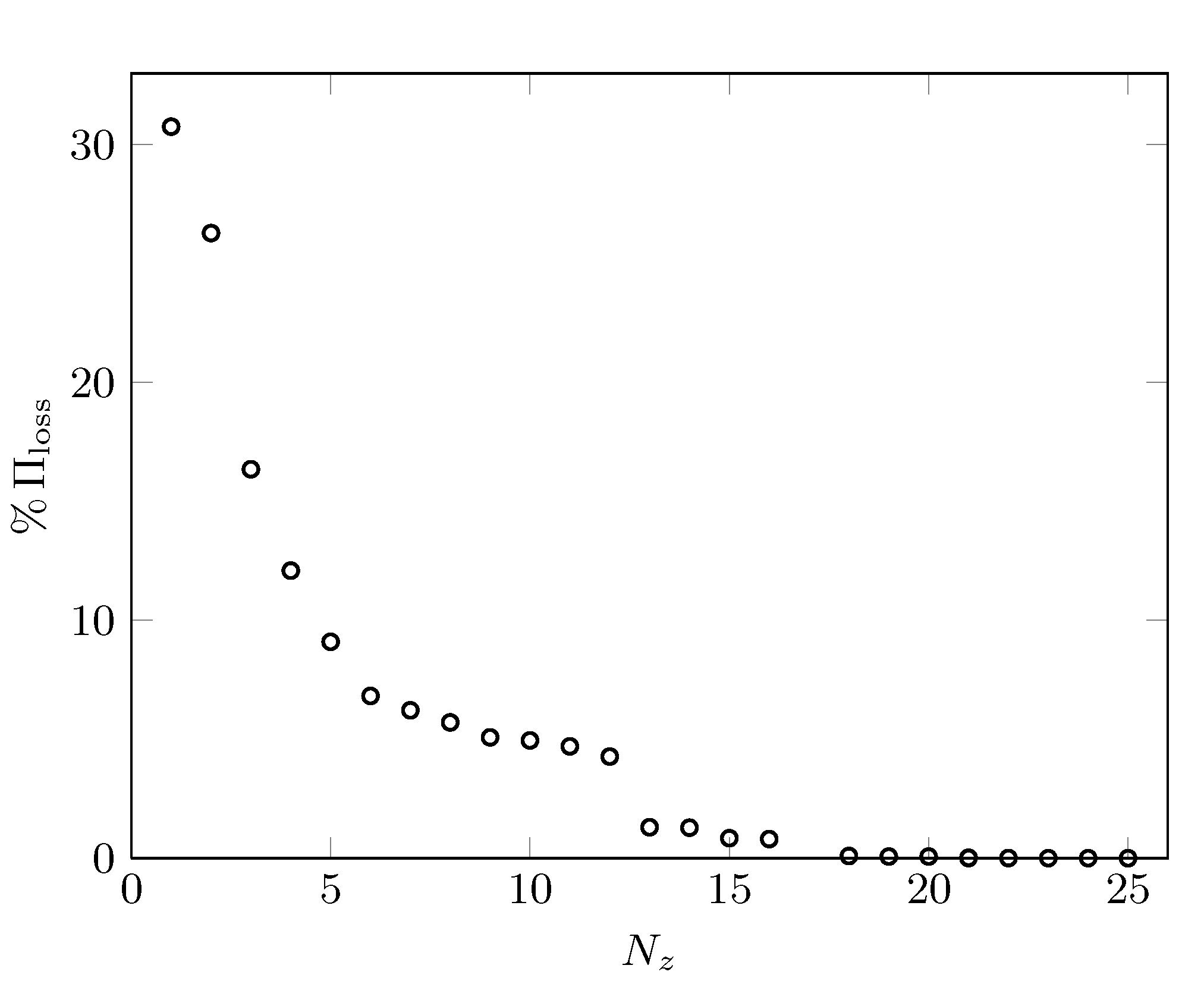 |
Performance loss,
|
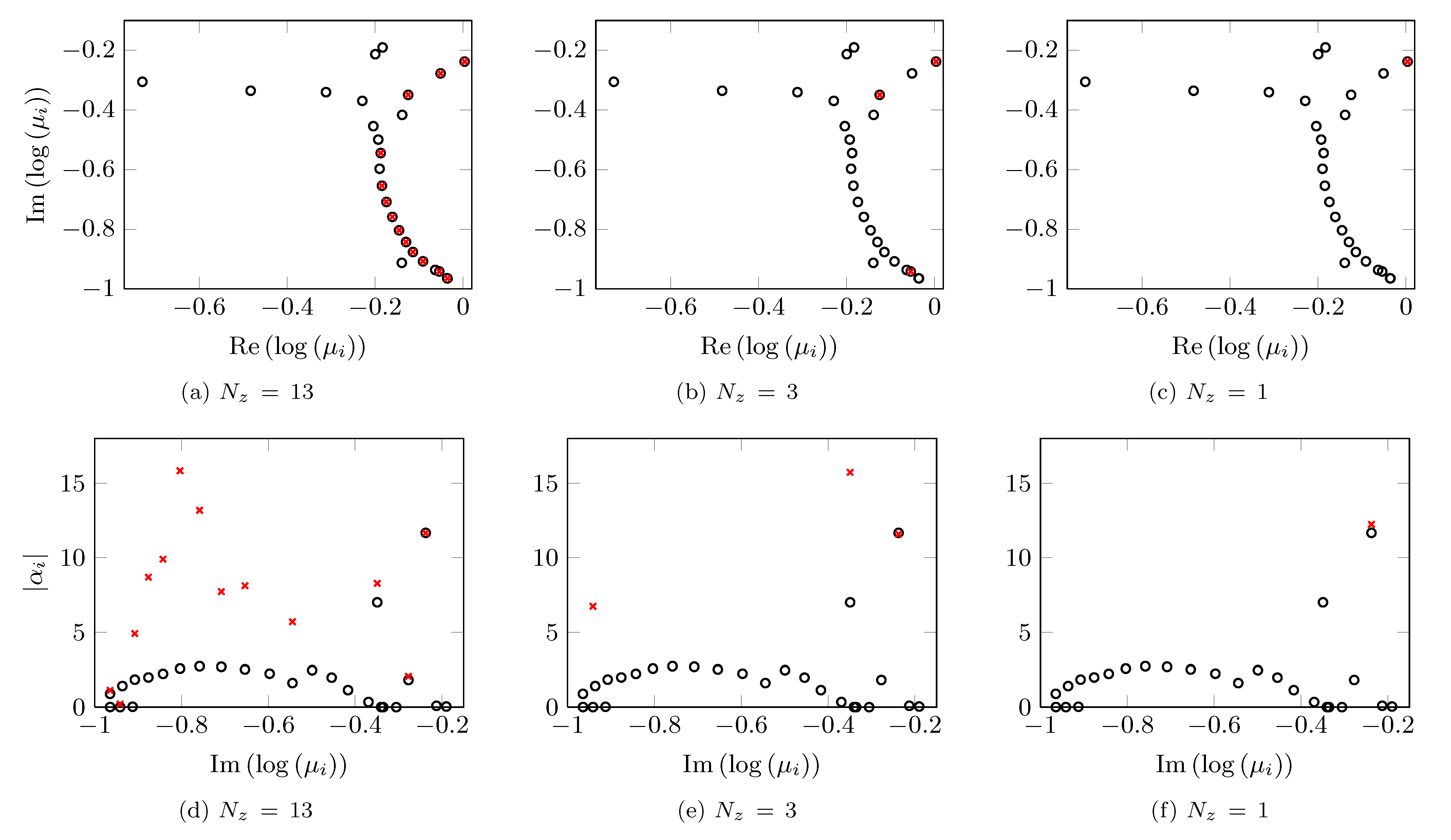 |
Eigenvalues of |
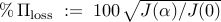 ,
of the optimal vector of amplitudes
,
of the optimal vector of amplitudes 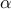 resulting from the
sparsity-promoting DMD algorithm with
resulting from the
sparsity-promoting DMD algorithm with 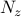 DMD modes.
DMD modes.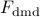 (first row) and the absolute values of
the DMD amplitudes
(first row) and the absolute values of
the DMD amplitudes 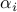 (second row). The results are obtained
using the standard DMD algorithm (circles) and the sparsity-promoting
DMD algorithm (crosses) with
(second row). The results are obtained
using the standard DMD algorithm (circles) and the sparsity-promoting
DMD algorithm (crosses) with