Flow through a cylinder bundle
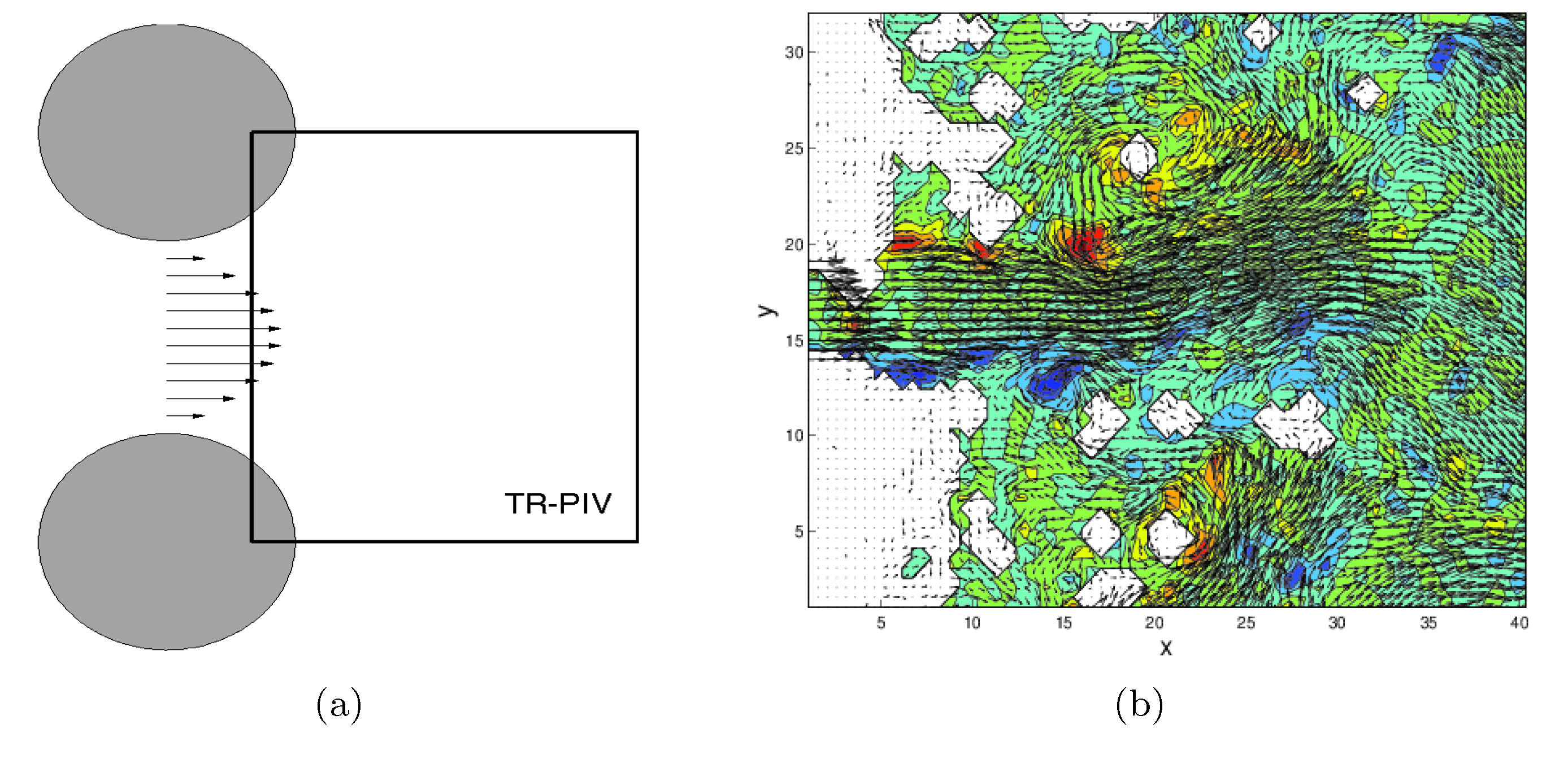 |
(a) Geometry of a flow between two cylinders along with the
interrogation window where time-resolved PIV measurements are taken.
This simple configuration inherits the main features from more complex
settings, including the presence of multiple, distinct frequencies and
the ‘‘flip-flop oscillations’’ of the exit stream.
|
Flow through cylinders in a bundle configuration is often encountered in the utility and energy conversion industry. Owing to their versatility and efficiency, cross-flow heat exchangers account for the vast majority of heat exchangers in oil refining, process engineering, petroleum extraction, and power generation sectors. Consequently, even a modest improvement in their effectiveness and operational margins would have a significant impact on production efficiency. In spite of their widespread use, the details of the flow (and heat transfer) through cylinder bundles are far from fully understood, thereby making this type of flow, along with its simplified variants, the subject of active research.
Vortex shedding and complex wake interactions can induce vibrations and structural resonances which, in turn, may result in fretting wear, collisional damage, material fatigue, creep, and ultimately in cracking. Even though the flow through a cylinder bundle is highly complicated, it is characterized by well-defined shedding frequencies. For single-row cylinders, only a few distinct frequencies are detected, while for more complex array configurations, a multitude of precise shedding frequencies are observed. The presence of distinct shedding frequencies makes this type of flow well-suited for a decomposition of the flow fields into single-frequency modes.
In addition to the multiple-frequency behavior, a characteristic oscillatory pattern – labelled as a ‘‘flip-flop phenomenon’’ – is typically observed in the exit stream of the flow through cylinder bundles. It consists of a meta-stable deflection of the exiting jet off the centerline location. A statistical analysis of the velocity field in a cross-stream section shows a strongly bimodal distribution. Over a wide range of Reynolds numbers, the Strouhal number associated with the oscillation between these two states is approximately Reynolds number independent. This flow feature can also be represented by a dynamic mode decomposition of the flow fields.
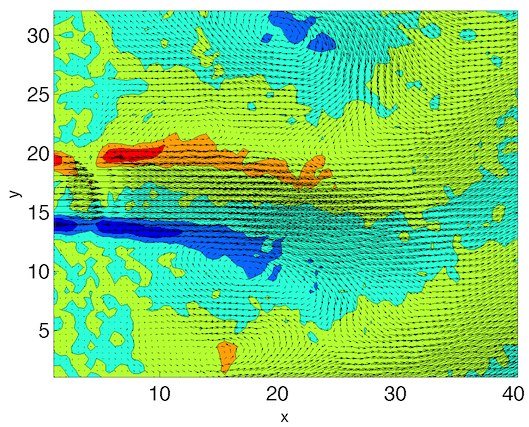 |
Snapshots of velocity vectors and vorticity contours resulting from a
sparse DMD representation (with |
 |
Dependence of the absolute value of the DMD amplitudes |
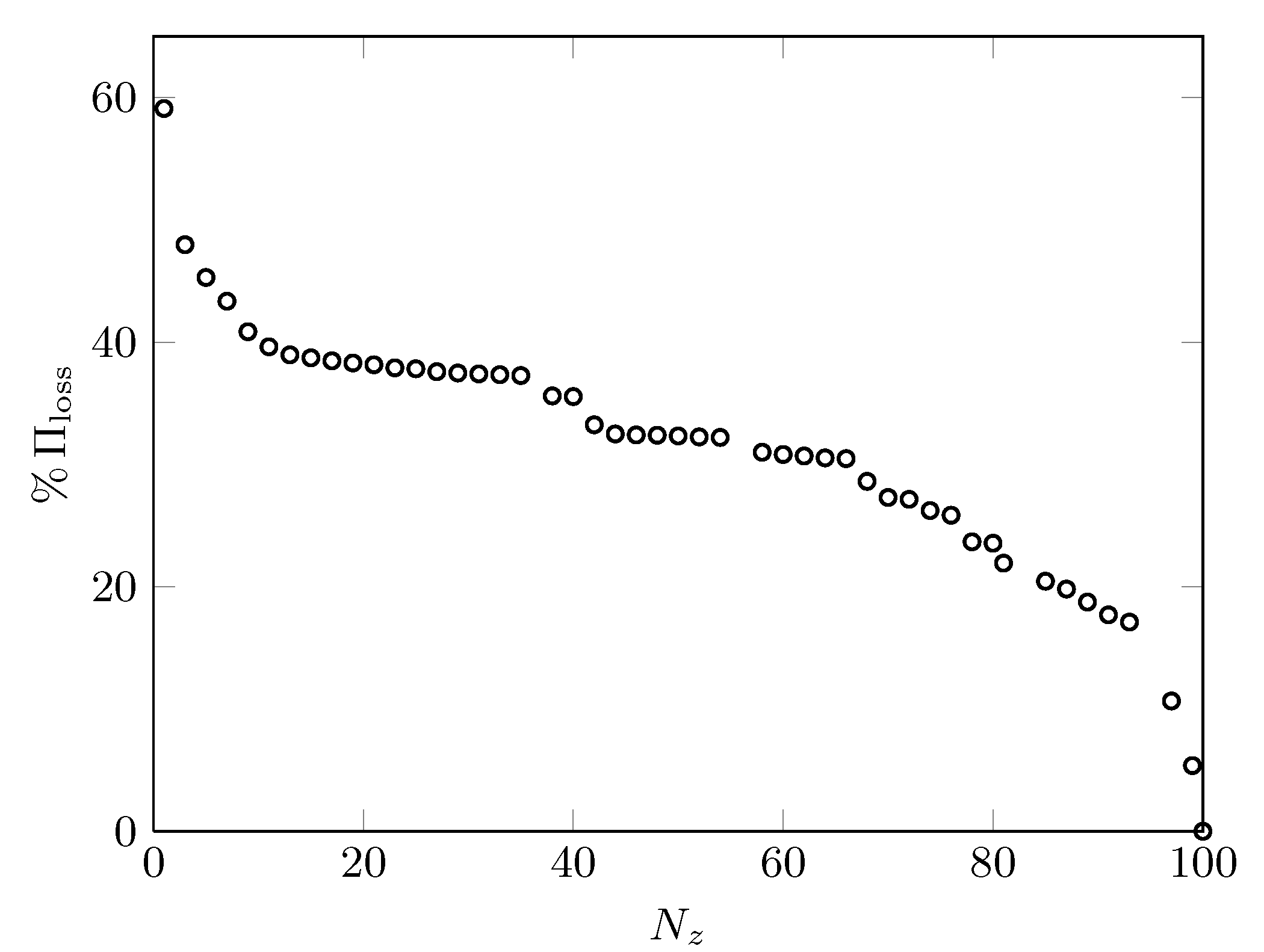 |
Performance loss,
|
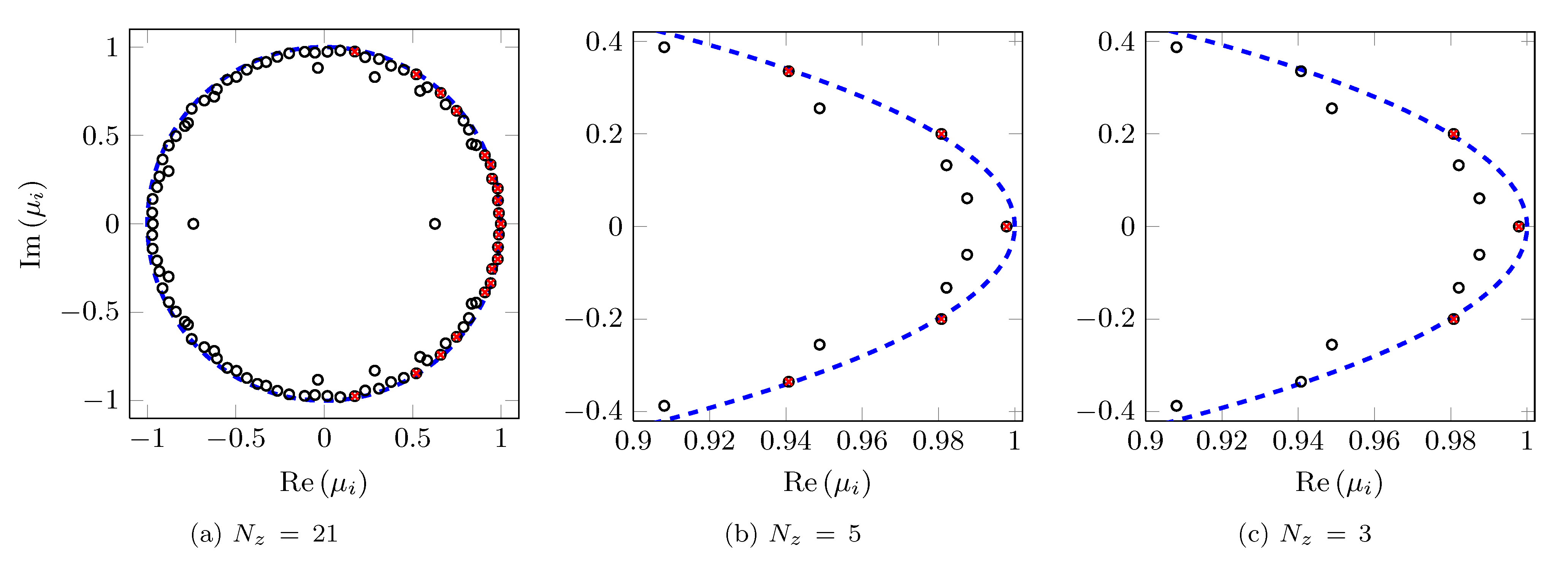 |
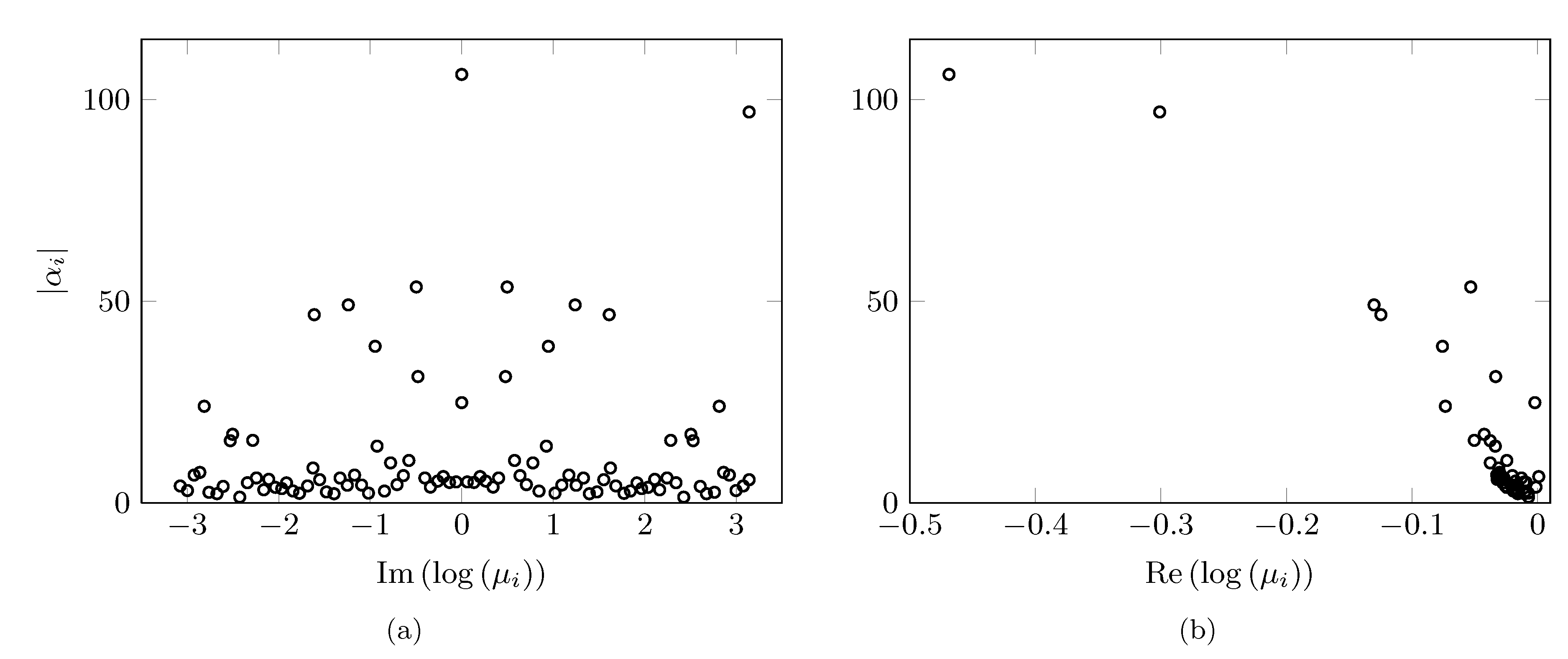
Eigenvalues resulting from the standard DMD algorithm (circles) along
with the subset of |
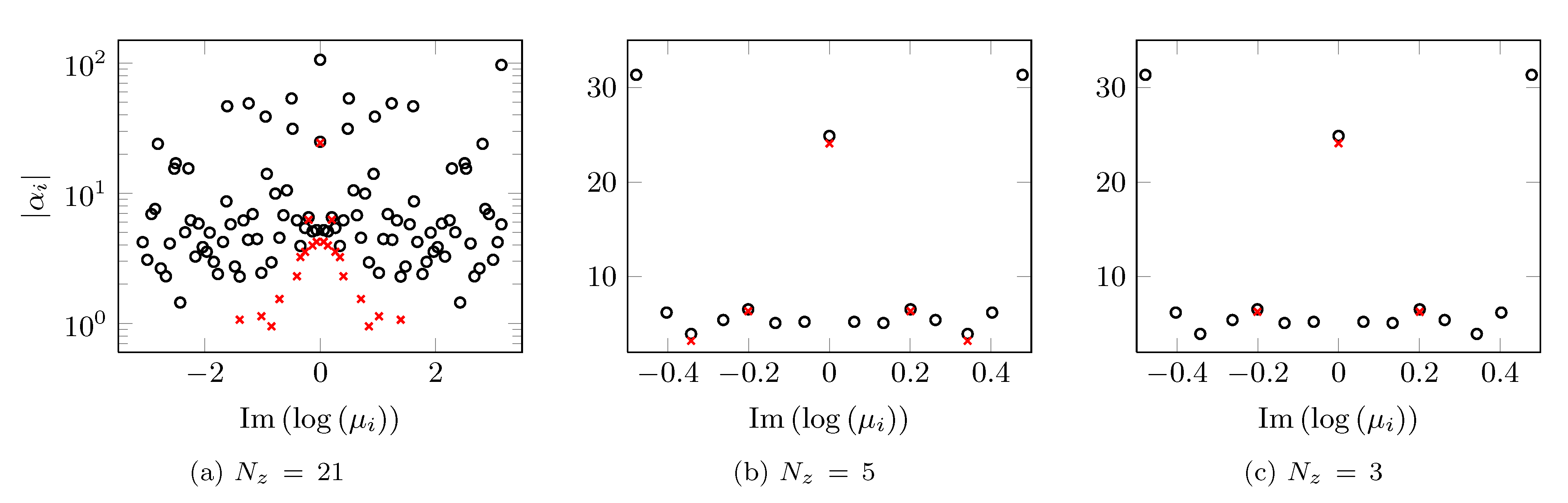 |
Dependence of the absolute value of the amplitudes |
Animation
An animation of the flow field resulting from a sparse DMD
representation (with 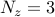 modes) of the full data sequence is shown
next. We observe a deflected jet and strong vortical components off the
symmetry axis. This animation has been obtained using the frequency
identified by the sparsity-promoting DMD algorithm
modes) of the full data sequence is shown
next. We observe a deflected jet and strong vortical components off the
symmetry axis. This animation has been obtained using the frequency
identified by the sparsity-promoting DMD algorithm 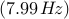 and it
reproduces the main features of the full data sequence, i.e., the
lateral swaying of the jet under the influence of the wake vortices of
the two cylinders.
and it
reproduces the main features of the full data sequence, i.e., the
lateral swaying of the jet under the influence of the wake vortices of
the two cylinders.
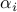 on (a)
the frequency and (b) the real part of the corresponding DMD eigenvalues
on (a)
the frequency and (b) the real part of the corresponding DMD eigenvalues
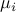 .
.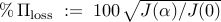 ,
of the optimal vector of amplitudes
,
of the optimal vector of amplitudes 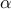 resulting from the
sparsity-promoting DMD algorithm with
resulting from the
sparsity-promoting DMD algorithm with 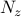 DMD modes.
DMD modes.