Sparsity-Promoting Dynamic Mode Decomposition
Mihailo R. Jovanovic, Peter J. Schmid, and Joseph W. Nichols
Abstract
Dynamic mode decomposition (DMD) represents an effective means for capturing the
essential features of numerically or experimentally generated flow fields. In
order to achieve a desirable tradeoff between the quality of approximation and
the number of modes that are used to approximate the given fields, we develop a
sparsity-promoting variant of the standard DMD algorithm. Sparsity is induced by
regularizing the least-squares deviation between the matrix of snapshots and the
linear combination of DMD modes with an additional term that penalizes the
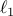-norm of the vector of DMD amplitudes. The globally optimal solution of
the resulting regularized convex optimization problem is computed using the
alternating direction method of multipliers, an algorithm well-suited for large
problems. Several examples of flow fields resulting from numerical simulations
and physical experiments are used to illustrate the effectiveness of the
developed method.
Reference
Sparsity-Promoting Dynamic Mode Decomposition
M. R. Jovanovic, P. J. Schmid, and J. W. Nichols
Phys. Fluids, vol. 26, no. 2, p. 024103 (22 pages), 2014.
 |