Leader Selection in Stochastically Forced Consensus Networks
 |
Fu Lin, Makan Fardad, and Mihailo R. Jovanovic June 2013 Matlab Files
Presentation
Papers
|
Purpose
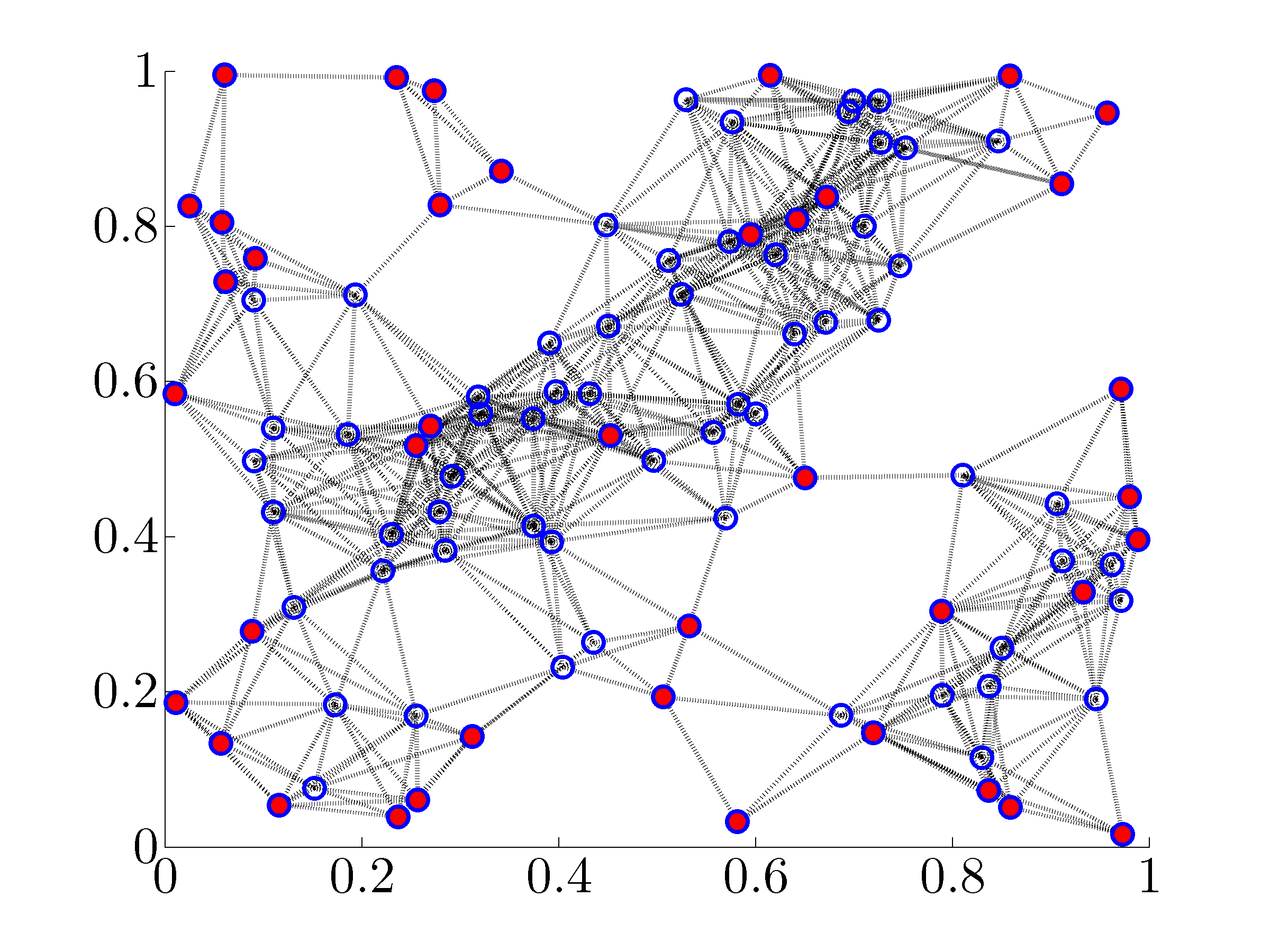
This website provides a Matlab implementation of algorithms that quantify suboptimality of solutions to two combinatorial network optimization problems. For undirected consensus networks, these problems arise in assignment of a pre-specified number of nodes, as leaders, in order to minimize the mean-square deviation from consensus. For distributed localization in sensor networks, one of our formulations is equivalent to the problem of choosing a pre-specified number of absolute position measurements among available sensors in order to minimize the variance of the estimation error.
Two combinatorial problems involving graph Laplacian
Diagonally strengthened graph Laplacian
Let 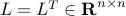 be the graph Laplacian of an undirected
connected network. A diagonally strengthened graph Laplacian is
obtained by adding a vector
be the graph Laplacian of an undirected
connected network. A diagonally strengthened graph Laplacian is
obtained by adding a vector 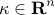 with positive
elements to the main diagonal of
with positive
elements to the main diagonal of 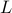 ,
,
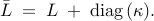
For connected graphs, the diagonally strengthened Laplacian 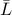 is
a positive definite matrix.
is
a positive definite matrix.
We are interested in selecting a pre-specified number 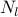 of diagonal
elements of
of diagonal
elements of 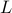 such that the trace of the inverse of the strengthened
graph Laplacian is minimized. This problem can be expressed as
such that the trace of the inverse of the strengthened
graph Laplacian is minimized. This problem can be expressed as
![begin{array}{lrcl} {rm minimize} & J(x) & = & {rm trace} left( (L ,+, {rm diag} , (kappa) , {rm diag} , (x) )^{-1} right) [0.25cm] {rm subject~to} & x_i & in & {0,1}, ~~~~~ i ; = ; 1,ldots,n [0.15cm] & displaystyle{sum_{i , = , 1}^n} , x_i & = & N_l end{array} ~~~~~~~ ({rm LS1})](eqs/4333843790813906010-130.png)
where the graph Laplacian 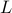 and the vector
and the vector  with positive
elements are problem data, and the Boolean-valued vector
with positive
elements are problem data, and the Boolean-valued vector 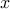 with
cardinality
with
cardinality 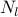 is the optimization variable.
is the optimization variable.
This combinatorial optimization problem is of interest in several
applications. For example, in leader-follower networks subject to
stochastic disturbances, the problem 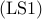 amounts to assigning
amounts to assigning
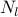 nodes as leaders (that have access to their own states) such that
the mean-square deviation from consensus is minimized. We refer to
nodes as leaders (that have access to their own states) such that
the mean-square deviation from consensus is minimized. We refer to
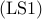 as the noise-corrupted leader selection
problem. Also, it can be shown that the problem of choosing
as the noise-corrupted leader selection
problem. Also, it can be shown that the problem of choosing 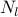 absolute position measurements among
absolute position measurements among 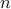 sensors in order to minimize
the variance of the estimation error in sensor networks is equivalent to
the problem
sensors in order to minimize
the variance of the estimation error in sensor networks is equivalent to
the problem 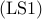 .
.
Principal submatrices of graph Laplacian
Let 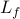 be a principal submatrix of the graph Laplacian
be a principal submatrix of the graph Laplacian 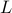 obtained by
deleting a pre-specified number
obtained by
deleting a pre-specified number 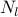 of rows and columns. For undirected
connected graphs,
of rows and columns. For undirected
connected graphs, 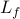 is a positive definite matrix.
is a positive definite matrix.
The problem of finding a principal submatrix 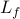 of
of 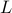 such that
such that
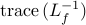 is minimized can be expressed as
is minimized can be expressed as
![begin{array}{lrcl} {rm minimize} & J_f(x) & = & {rm trace} , (L_f^{-1}) [0.25cm] {rm subject~to} & x_i & in & {0,1}, ~~~~~ i ; = ; 1,ldots,n [0.15cm] & displaystyle{sum_{i , = , 1}^n} , x_i & = & N_l end{array} ~~~~~~~ ({rm LS2})](eqs/6253127923021460596-130.png)
where the Boolean-valued vector 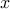 with cardinality
with cardinality 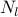 is the
optimization variable. The index set of nonzero elements of
is the
optimization variable. The index set of nonzero elements of 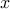 identifies the rows and columns of the graph Laplacian
identifies the rows and columns of the graph Laplacian 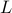 that need to
be deleted in order to obtain
that need to
be deleted in order to obtain 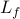 .
.
Similar to 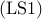 , the combinatorial optimization problem
, the combinatorial optimization problem 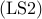 arises in several applications. For example, in leader-follower
networks, the problem
arises in several applications. For example, in leader-follower
networks, the problem 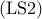 amounts to assigning
amounts to assigning 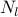 nodes as
leaders (that perfectly follow their desired trajectories) such that the
mean-square deviation from consensus is minimized. We refer to
nodes as
leaders (that perfectly follow their desired trajectories) such that the
mean-square deviation from consensus is minimized. We refer to 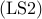 as the noise-free leader selection problem.
as the noise-free leader selection problem.
Performance bounds on the global optimal value
For large graphs, it is challenging to determine global solutions to the
combinatorial optimization problems 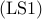 and
and 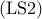 .
Instead, we develop efficient algorithms that quantify performance
bounds on the global optimal values. Specifically, we obtain lower
bounds by solving convex relaxations of
.
Instead, we develop efficient algorithms that quantify performance
bounds on the global optimal values. Specifically, we obtain lower
bounds by solving convex relaxations of 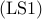 and
and 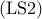 and we obtain upper bounds using a simple but efficient greedy
algorithm. We note that the greedy approach also provides feasible
points of
and we obtain upper bounds using a simple but efficient greedy
algorithm. We note that the greedy approach also provides feasible
points of 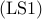 and
and 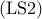 .
.
Lower bounds from convex relaxations
Since the objective function 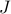 in
in 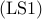 is the composition of a
convex function
is the composition of a
convex function 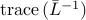 of a positive definite matrix
of a positive definite matrix
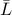 with an affine function
with an affine function 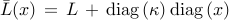 ,
it follows that
,
it follows that  is a convex function of
is a convex function of  . By enlarging the
Boolean constraint set
. By enlarging the
Boolean constraint set  to its convex hull
to its convex hull ![x_{i} in [0,1]](eqs/4967989987547363488-130.png) , we obtain the following convex relaxation of
, we obtain the following convex relaxation of 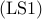 :
:
![begin{array}{lrcl} {rm minimize} & J(x) & = & {rm trace} left( (L ,+, {rm diag} , (kappa) , {rm diag} , (x) )^{-1} right) [0.25cm] {rm subject~to} & x_i & in & [0,1], ~~~~~ i ; = ; 1,ldots,n [0.15cm] & displaystyle{sum_{i , = , 1}^n} , x_i & = & N_l end{array} ~~~~~~~ ({rm CR1})](eqs/3211014161622629344-130.png)
Schur complement can be used to cast 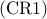 as a semidefinite
program (SDP). Thus,
as a semidefinite
program (SDP). Thus, 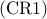 can be solved using general-purpose
SDP solvers with computational complexity of order
can be solved using general-purpose
SDP solvers with computational complexity of order 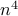 . In contrast,
computational complexity of a customized interior point method that we
develop is of order
. In contrast,
computational complexity of a customized interior point method that we
develop is of order 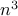 .
.
In contrast to 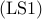 , the objective function
, the objective function 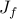 in
in 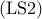 is a nonconvex function of
is a nonconvex function of 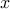 . By a change of optimization variables, we
identify the source of nonconvexity in the form of a rank constraint.
Removal of the rank constraint and relaxation of the Boolean constraints can
be used to obtain the following convex relaxation of
. By a change of optimization variables, we
identify the source of nonconvexity in the form of a rank constraint.
Removal of the rank constraint and relaxation of the Boolean constraints can
be used to obtain the following convex relaxation of 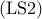 :
:
![begin{array}{lrcl} {rm minimize} & J_f(Y,y) & = & {rm trace} left( ( L circ Y ,+, {rm diag} left( {bf 1} - y right) )^{-1} right) ,-, N_l [0.25cm] {rm subject~to} & y_i & in & [0,1], ~~~~~ i ; = ; 1,ldots,n [0.15cm] & Y_{ij} & in & [0,1], ~~~~~ i,j ; = ; 1,ldots,n [0.15cm] & displaystyle{sum_{i,=,1}^n} ~ y_i & = & N_f, ~~~~~ displaystyle{sum_{i,j,=,1}^n} ~Y_{ij} ~ = ~ N_f^2 [0.25cm] & Y & succeq & 0 end{array} ~~~~~~~ ({rm CR2})](eqs/3968119729463796375-130.png)
Here, the symmetric matrix 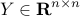 and the vector
and the vector
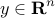 are the optimization variables,
are the optimization variables,  is the
elementwise multiplication of two matrices,
is the
elementwise multiplication of two matrices, 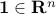 is
the vector of all ones, and the integer
is
the vector of all ones, and the integer 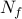 is given by
is given by 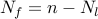 .
.
Similar to 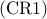 , the convex relaxation
, the convex relaxation 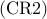 can be
cast as an SDP and solved using general-purpose SDP solvers. However,
since this approach requires the computational complexity of order
can be
cast as an SDP and solved using general-purpose SDP solvers. However,
since this approach requires the computational complexity of order
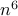 , we develop an alternative approach that is well-suited for large
problems. Our approach relies on the use of the alternating direction
method of multipliers (ADMM) which allows us to decompose
, we develop an alternative approach that is well-suited for large
problems. Our approach relies on the use of the alternating direction
method of multipliers (ADMM) which allows us to decompose 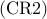 into a sequence of subproblems that can be solved with
into a sequence of subproblems that can be solved with 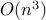 operations.
operations.
Upper bounds using a greedy algorithm
With lower bounds on the global optimal value resulting from the convex
relaxations 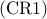 and
and 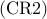 , we use a greedy algorithm
to compute upper bounds. This algorithm selects one leader at a time by
assigning the node that provides the largest performance improvement as
the leader. Once this is done, an attempt to improve a selection of
, we use a greedy algorithm
to compute upper bounds. This algorithm selects one leader at a time by
assigning the node that provides the largest performance improvement as
the leader. Once this is done, an attempt to improve a selection of
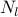 leaders is made by checking possible swaps between the leaders and
the followers. In both steps, substantial improvement in algorithmic
complexity is achieved by exploiting structure of the low-rank
modifications to Laplacian matrices.
leaders is made by checking possible swaps between the leaders and
the followers. In both steps, substantial improvement in algorithmic
complexity is achieved by exploiting structure of the low-rank
modifications to Laplacian matrices.
Detailed description of the aforementioned algorithms (i.e., the greedy
algorithm, the customized interior point method for 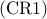 , and the
ADMM-based algorithm for
, and the
ADMM-based algorithm for 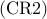 ) are provided in our paper
) are provided in our paper
Algorithms for Leader Selection in Stochastically Forced Consensus Networks
F. Lin, M. Fardad, and M. R. Jovanovic
IEEE Trans. Automat. Control, 2013, conditionally accepted; also arXiv:1302.0450.
Description of the main function
>> [Jlow,Jup,x] = leaders(L,Nl,kappa,flag);
Our Matlab function leaders.m takes the graph Laplacian 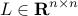 , the positive integer
, the positive integer 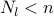 , the vector
, the vector 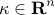 with positive elements, and the indicator variable
with positive elements, and the indicator variable
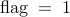 – for the noise-corrupted leader selection formulation
– for the noise-corrupted leader selection formulation 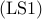 ;
;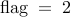 – for the noise-free leader selection formulation
– for the noise-free leader selection formulation 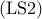 .
.
leaders.m returns the lower and upper bounds on the global optimal
value of the leader selection problem 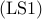 or
or 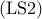 ,
along with the Boolean-valued vector
,
along with the Boolean-valued vector 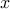 which represents a feasible
point for the selection of leaders.
which represents a feasible
point for the selection of leaders.
Acknowledgements
This project is supported in part by the National Science Foundation under
CAREER Award CMMI-0644793
Award CMMI-0927509
Award CMMI-0927720.