Design of Optimal Sparse Feedback Gains via
the Alternating Direction Method of Multipliers
Fu Lin, Makan Fardad, and Mihailo R. Jovanovic
Abstract
We design sparse and block sparse feedback gains that minimize the
variance amplification (i.e., the 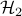 norm) of distributed
systems. Our approach consists of two steps. First, we identify sparsity
patterns of feedback gains by incorporating sparsity-promoting penalty
functions into the optimal control problem, where the added terms
penalize the number of communication links in the distributed
controller. Second, we optimize feedback gains subject to structural
constraints determined by the identified sparsity patterns. In the first
step, the sparsity structure of feedback gains is identified using the
alternating direction method of multipliers, which is a powerful
algorithm well-suited to large optimization problems. This method
alternates between promoting the sparsity of the controller and
optimizing the closed-loop performance, which allows us to exploit the
structure of the corresponding objective functions. In particular, we
take advantage of the separability of the sparsity-promoting penalty
functions to decompose the minimization problem into sub-problems that
can be solved analytically. Several examples are provided to illustrate
the effectiveness of the developed approach.
norm) of distributed
systems. Our approach consists of two steps. First, we identify sparsity
patterns of feedback gains by incorporating sparsity-promoting penalty
functions into the optimal control problem, where the added terms
penalize the number of communication links in the distributed
controller. Second, we optimize feedback gains subject to structural
constraints determined by the identified sparsity patterns. In the first
step, the sparsity structure of feedback gains is identified using the
alternating direction method of multipliers, which is a powerful
algorithm well-suited to large optimization problems. This method
alternates between promoting the sparsity of the controller and
optimizing the closed-loop performance, which allows us to exploit the
structure of the corresponding objective functions. In particular, we
take advantage of the separability of the sparsity-promoting penalty
functions to decompose the minimization problem into sub-problems that
can be solved analytically. Several examples are provided to illustrate
the effectiveness of the developed approach.
Reference
Design of optimal sparse feedback gains via the alternating direction method of multipliers
F. Lin, M. Fardad, and M. R. Jovanovic
IEEE Trans. Automat. Control, vol. 58, no. 9, pp. 2426-2431, September 2013.