Mass-spring system
 |
Mass-spring system with |
For the system with 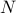 masses on a line, the state vector is determined by
masses on a line, the state vector is determined by
![x , = , left[ ; p^T ~, v^T ; right]^T](eqs/4451493342761316260-130.png) , where
, where 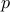 and
and  denote the vectors of positions
and velocities of all masses. Setting all masses and spring constants to unity and
partitioning matrices in the state-space representation conformably with the partition
of
denote the vectors of positions
and velocities of all masses. Setting all masses and spring constants to unity and
partitioning matrices in the state-space representation conformably with the partition
of 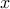 yields
yields
![A ; = ; left[ begin{array}{cc} O & I T & O end{array} right], ~~ B_1 ; = ; B_2 ; = ; left[ begin{array}{cc} O I end{array} right], ~~ Q ; = ; left[ begin{array}{cc} I & O O & I end{array} right], ~~ R ; = ; 10I.](eqs/7613512838734132229-130.png)
where 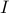 and
and 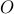 are
are 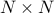 identity
and zero matrices, and
identity
and zero matrices, and 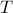 is a tridiagonal symmetric Toeplitz matrix with
is a tridiagonal symmetric Toeplitz matrix with 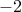 on the main diagonal
and
on the main diagonal
and 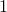 on the first upper and lower sub-diagonals, e.g.,
on the first upper and lower sub-diagonals, e.g.,
![T ; sim ; left[ begin{array}{rrrr} -2 & 1 & 0 & 0 1 & -2 & 1 & 0 0 & 1 & -2 & 1 0 & 0 & 1 & -2 end{array} right].](eqs/9055004590998915540-130.png)
In the absence of sparsity constraints, i.e., at 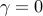 , the optimal
, the optimal  controller
controller
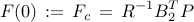
is obtained from the positive definite solution of the algebraic Riccati equation
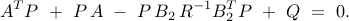
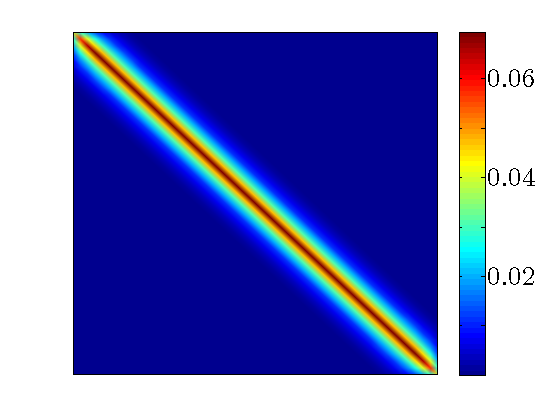 |
The optimal centralized position feedback gain matrix |
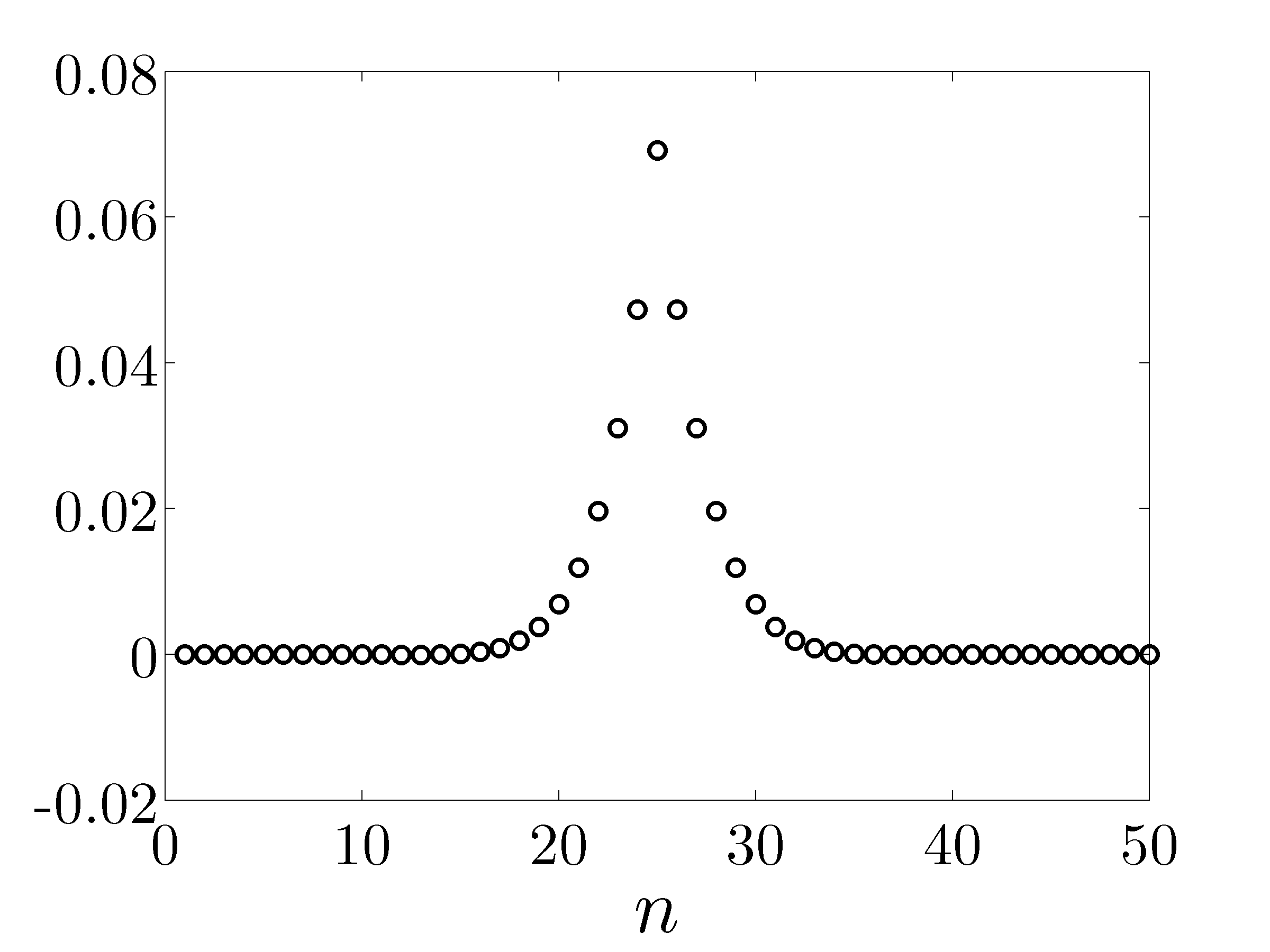 |
Optimal centralized position gains for the middle mass |
Localization can be enforced by truncating the optimal centralized controller.
This, however, may introduce performance degradation and even instability of the closed-loop system.
(Additional information is provided in the Network with 100 unstable nodes example.)
Instead of using simple truncation, the alternating direction method of multipliers enforces sparsity
in the 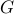 -minimization step and improves the quadratic performance in the
-minimization step and improves the quadratic performance in the
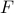 -minimization step. This mechanism of alternating between promoting sparsity and optimizing
the quadratic performance plays an important role in striking a balance between these two
competing objectives.
-minimization step. This mechanism of alternating between promoting sparsity and optimizing
the quadratic performance plays an important role in striking a balance between these two
competing objectives.
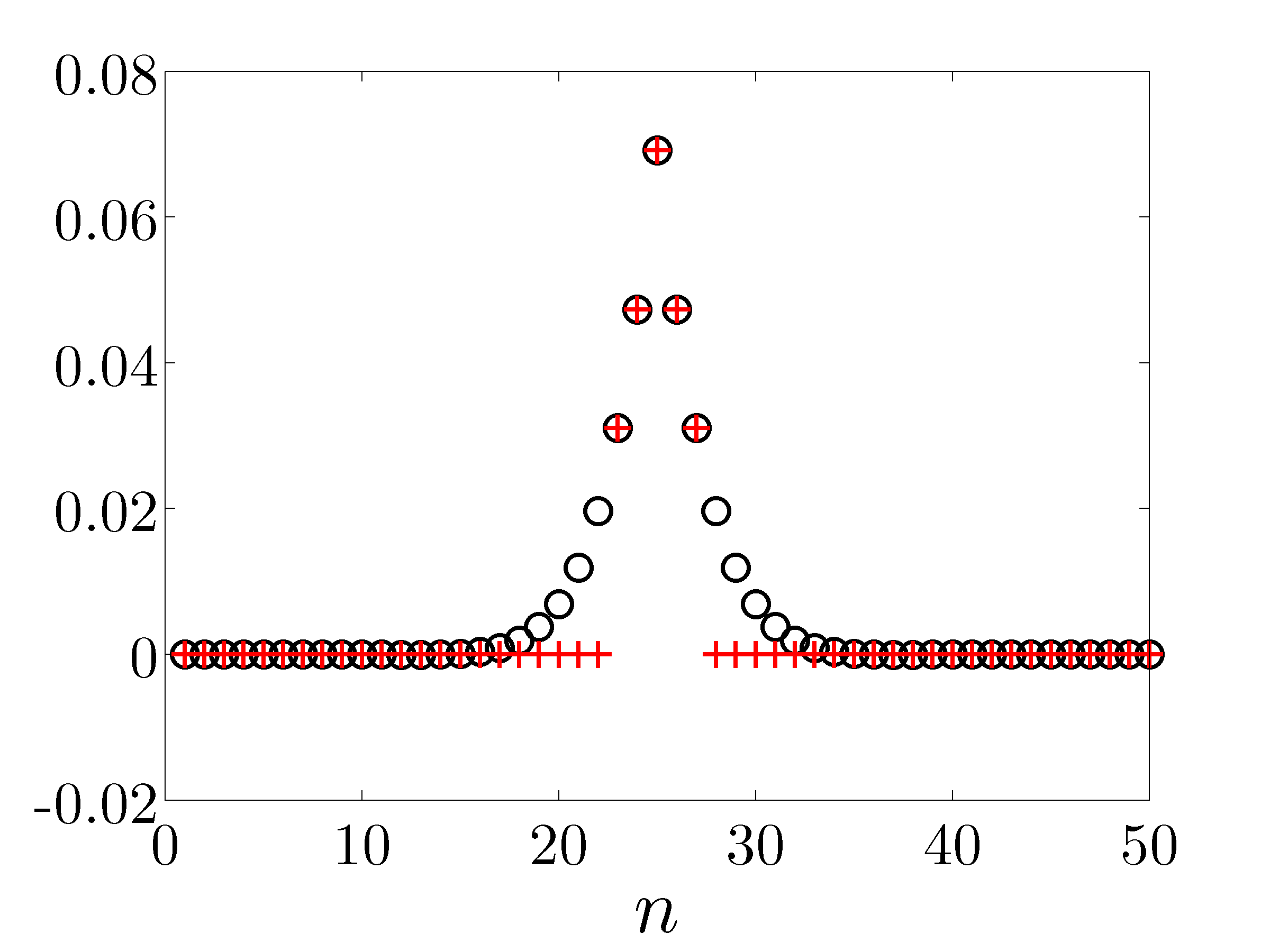 |
An example of truncation: all but five largest elements of the optimal centralized position gain are set to zero. The resulting controller will only use the position measurements of the mass on which it acts and of the two neighboring masses to the left and to the right. |
For illustration, we use cardinality function, weighted 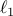 norm, and sum-of-logs
as the sparsity-promoting penalty functions. For all three cases, the optimal position and
velocity feedback gains become diagonal matrices for large values of
norm, and sum-of-logs
as the sparsity-promoting penalty functions. For all three cases, the optimal position and
velocity feedback gains become diagonal matrices for large values of 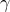 . It is noteworthy that
the optimal sparse feedback gain, with only
. It is noteworthy that
the optimal sparse feedback gain, with only 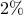 of nonzero elements relative to the optimal
centralized controller
of nonzero elements relative to the optimal
centralized controller 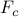 , introduces performance loss of only
, introduces performance loss of only 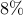 (compared to
(compared to 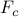 ).
).
The following links contain Matlab codes and computational results for each case.
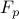 in the mass-spring system with
in the mass-spring system with  masses.
Both
masses.
Both 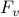 in
in ![F_c = [F_p ~, F_v]](eqs/344924658870420228-130.png) have almost constant diagonals (modulo edges)
and exponential off-diagonal decay.
have almost constant diagonals (modulo edges)
and exponential off-diagonal decay.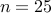 .
.